10. Sınıf Matematik Ders Kitabı Sayfa 303 Cevapları Meb Yayınları

10. Sınıf Matematik Ders Kitabı Cevapları | MEB Yayınları | Sayfa 303 – Araştırma Ödevi
Soru: Aşağıda verilen adımları gerçekleştirerek araştırma ödevini 10 gün içinde eksiksiz olarak tamamlayınız.
Bu araştırma ödevinde ters orantı içeren gerçek yaşam problemleri incelenir, rasyonel fonksiyon ile modellenir, tablo ve grafik oluşturulur ve sonuçlar rapor ile sunum hâline getirilir.
1) Gerçek yaşamdan uygun problem seçimi
Ödevin temel amacı, rasyonel referans fonksiyonların gerçek hayatta ters orantı ilişkisini nasıl modellediğini göstermektir. Aşağıdaki örnekler bu amaca uygundur:
- İşçi sayısı – işin bitme süresi
- Araç hızı – varış süresi
- Musluk sayısı – havuzun dolma süresi
- Makine sayısı – üretim süresi
Bu ödev için en anlaşılır ve günlük hayata en uygun örnek, işçi sayısı ile işin bitme süresi arasındaki ilişkidir.
2) Bağımsız ve bağımlı değişkenlerin belirlenmesi
- Bağımsız değişken (x): İşçi sayısı
- Bağımlı değişken (y): İşin tamamlanma süresi (gün)
İşçi sayısı arttıkça, işin bitme süresi azalır. Bu durum ters orantı olduğunu gösterir.
3) Veri tablosunun oluşturulması
Toplam yapılacak iş miktarı sabit kabul edilir. Örneğin iş miktarı 240 iş-gün olsun.
Bu durumda ilişki: y = 240 / x
| İşçi Sayısı (x) | İşin Bitme Süresi (y – gün) |
|---|---|
| 4 | 60 |
| 6 | 40 |
| 8 | 30 |
| 10 | 24 |
| 12 | 20 |
| 15 | 16 |
| 20 | 12 |
4) Fonksiyonun cebirsel temsili ve grafik yorumu
- Fonksiyon: y = 240 / x
- Bu fonksiyon rasyonel fonksiyon türündedir.
- Grafik azalan yapıdadır.
- İşçi sayısı arttıkça, geçen süre giderek azalır.
- Grafik 1. bölgede yer alır ve eksenlere yaklaşır fakat kesmez.
5) Tanım ve değer aralıklarının belirlenmesi
Gerçek hayata uygunluk açısından sınırlama yapılmalıdır:
- Tanım Kümesi: x ∈ [4, 20] (işçi sayısı 0 olamaz, çok yüksek de olamaz)
- Değer Kümesi: y ∈ [12, 60] (en kısa ve en uzun süreler)
Bu aralıklar, problemin gerçek yaşamla uyumlu olmasını sağlar.
6) Rapor hazırlama (öğretmen için ideal düzen)
Hazırlanacak rapor şu başlıklardan oluşmalıdır:
- Araştırmanın Amacı
- Seçilen Problem Durumu
- Bağımsız ve Bağımlı Değişkenler
- Veri Tablosu
- Fonksiyonun Cebirsel Modeli
- Grafik ve Yorumu
- Tanım ve Değer Aralıkları
- Sonuç ve Değerlendirme
7) Sunum önerisi (kısa ve etkili)
Sunumun anlaşılır olması için:
- 4–5 slayt yeterlidir
- Grafik mutlaka görsel olarak gösterilmelidir
- Son slaytta ters orantı vurgusu yapılmalıdır
10. Sınıf Matematik Ders Kitabı (MEB) Sayfa 303 – 19. Sıra Sizde Cevapları
Soru : Grup çalışması yapabilmek için öğretmeniniz rehberliğinde sınıfta üç gruba ayrılınız. Aşağıda verilen problem durumunu inceleyiniz ve soruları cevaplandırınız.
“İhtiyoloji (balık bilimi) alanında çalışan bir araştırmacı, Bafa Gölü ve Gediz Nehri’nde bulunan yılan balığı sayılarını,
x: 1 m³ suda yaşayan yılan balığı sayısı olmak üzere;
Bafa Gölü için f(x) = 2x² + 5x,
Gediz Nehri için g(x) = x² + 11x − 8 fonksiyonlarıyla modellemiştir.
Buna göre Gediz Nehri’nde bulunan yılan balığı sayısının, Bafa Gölü’nde bulunan yılan balığı sayısından fazla olması için 1 m³ suda yaşayan kaç tane yılan balığı olmalıdır?”
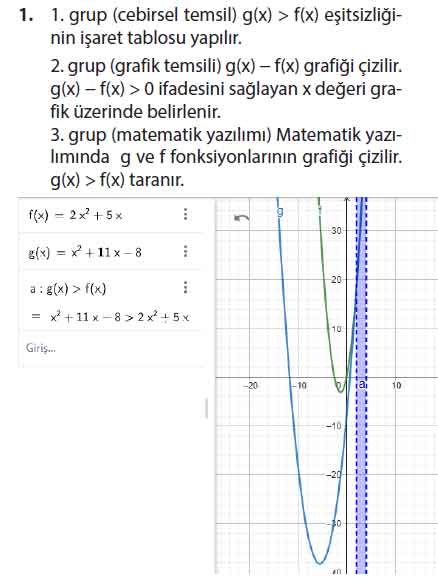
Soru 1) Problemi çözmek için gerekli çözüm stratejisini oluşturunuz.
- Amaç: Gediz Nehri’ndeki yılan balığı sayısının daha fazla olması → g(x) > f(x) koşulu kurulur.
- Yöntem 1 (Cebirsel): Fonksiyonlar karşılaştırılarak eşitsizlik çözülür.
- Yöntem 2 (Grafik): g(x) ve f(x) grafiklerinin kesişimleri ve üstünlük durumu incelenir.
- Yöntem 3 (Matematik Yazılımı): Eşitsizlik yazılıma girilerek çözüm doğrulanır.
- Son adım: “Kaç tane” ifadesi geçtiği için tam sayı çözüm belirlenir.
Soru 2) Oluşturduğunuz stratejiyi kullanarak problemi çözünüz.
Cevap (Cebirsel Çözüm):
Gediz Nehri’nin daha fazla olması için: g(x) > f(x)
x² + 11x − 8 > 2x² + 5x
Tüm terimleri bir tarafa alalım:
0 > x² − 6x + 8
Bu eşitsizlik: x² − 6x + 8 < 0
Çarpanlara ayıralım: (x − 2)(x − 4) < 0
Bu ifade 2 ile 4 arasında negatiftir:
2 < x < 4
x, 1 m³ suda yaşayan yılan balığı sayısını ifade ettiğinden tam sayı olmalıdır.
x = 3
Sonuç: 1 m³ suda yaşayan yılan balığı sayısı 3 olursa, Gediz Nehri’ndeki yılan balığı sayısı Bafa Gölü’ndekinden fazla olur.
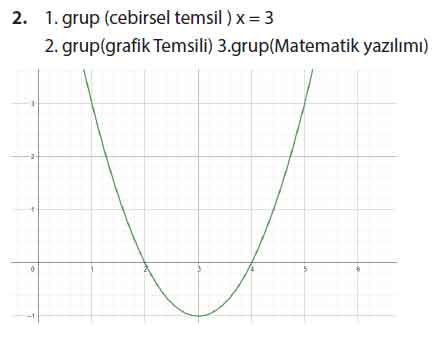
Soru 3) Kullanılan yöntemleri karşılaştırarak çözümleri doğrulayınız.
- Cebirsel yöntem, sonucu açık ve net biçimde verir (2 < x < 4 → x = 3).
- Grafik yöntemi, g(x) eğrisinin f(x) eğrisinin üzerinde kaldığı aralığı görsel olarak gösterir.
- Matematik yazılımı, hızlı ve hatasız bir doğrulama sağlar.
Değerlendirme: Sınav ve işlem doğruluğu açısından cebirsel yöntem en kullanışlıdır. Grafik ve yazılım yöntemleri ise sonucu kontrol etmek ve görselleştirmek için oldukça etkilidir.






Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.