10. Sınıf Matematik Ders Kitabı Sayfa 317 Cevapları Meb Yayınları

10. Sınıf Matematik Ders Kitabı Cevapları (MEB) – Sayfa 317
1. Sıra Sizde | Sayma Stratejileri Cevapları
Aşağıda Sayfa 317 – 1. Sıra Sizde etkinliği, sorular tam yazılarak, kısa–öz cevap + ayrıntılı açıklama şeklinde hazırlanmıştır.
Önemli noktalar koyu yazılmıştır.
Soru 1: Mete 2 farklı renkte ayakkabı, 3 farklı renkte pantolon, 4 farklı renkte gömlek ile kaç farklı kombin yapabileceğini hesaplamak istemektedir. Buna göre;
a) Mete’nin kaç farklı kombin yapabileceğini tablo yöntemi ve çizge yöntemi kullanarak belirleyiniz.
b) Mete’nin çarpma yoluyla sayma yöntemini kullanarak kaç farklı kombin yapabileceğini hesaplayınız. Sonucu önceki adımda tablo ve çizge yönteminde bulduğunuz sonuçlarla karşılaştırınız.
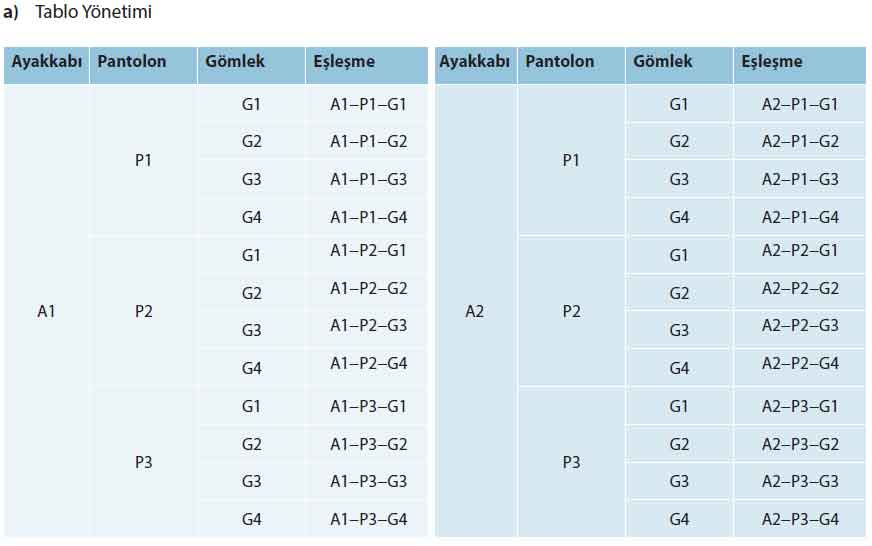
a) Tablo Yöntemi ve Çizge Yöntemi ile Kombin Hesaplama
Kısa Cevap: Mete toplamda 24 farklı kombin yapabilir.
Mete’nin kombin yapabileceği seçenekler:
- 2 farklı renkte ayakkabı: A1, A2
- 3 farklı renkte pantolon: P1, P2, P3
- 4 farklı renkte gömlek: G1, G2, G3, G4
İlk olarak tablo yöntemiyle hesaplayalım:
| Ayakkabı | Pantolon | Gömlek | Eşleşme |
|---|---|---|---|
| P1 | G1 | A1–P1–G1 | |
| G2 | A1–P1–G2 | ||
| G3 | A1–P1–G3 | ||
| G4 | A1–P1–G4 | ||
| G1 | A1–P2–G1 | ||
| G2 | A1–P2–G2 | ||
| G3 | A1–P2–G3 | ||
| G4 | A1–P2–G4 | ||
| G1 | A1–P3–G1 | ||
| G2 | A1–P3–G2 | ||
| G3 | A1–P3–G3 | ||
| G4 | A1–P3–G4 | ||
| P2 | G1 | A2–P1–G1 | |
| G2 | A2–P1–G2 | ||
| G3 | A2–P1–G3 | ||
| G4 | A2–P1–G4 | ||
| G1 | A2–P2–G1 | ||
| G2 | A2–P2–G2 | ||
| G3 | A2–P2–G3 | ||
| G4 | A2–P2–G4 | ||
| G1 | A2–P3–G1 | ||
| G2 | A2–P3–G2 | ||
| G3 | A2–P3–G3 | ||
| G4 | A2–P3–G4 |
Sonuç: Her ayakkabı için 12 farklı kombin vardır (3 pantolon × 4 gömlek).
Toplamda 24 farklı kombin yapılabilir.
Detaylı Cevap – Çizge (Ağaç Diyagramı) Yöntemi
Bir çizge (ağaç diyagramı) oluşturarak seçenekleri görselleştirebiliriz:
- İlk adımda: Ayakkabılar (A1 ve A2)
- İkinci adımda: Her ayakkabıya 3 pantolon (P1, P2, P3) eklenir.
- Son adımda: Her pantolona 4 gömlek (G1, G2, G3, G4) eklenir.
Ağaç diyagramında tüm dallar 24 farklı kombin oluşturur.

b) Çarpma Yoluyla Sayma Yöntemi
Kısa Cevap: Çarpma yöntemiyle 24 farklı kombin yapılabilir.
Çarpma yoluyla sayma yönteminde:
- Ayakkabı sayısı: 2
- Pantolon sayısı: 3
- Gömlek sayısı: 4
Bu sayıları çarptığımızda: 2×3×4=24
Sonuç: Toplamda 24 farklı kombin mümkündür.
Tablo ve çizge yöntemleriyle aynı sonuca ulaşılmıştır.







Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.