9. Sınıf Matematik 1. Ders Kitabı Sayfa 174-175 Cevapları Meb Yayınları

9. Sınıf Matematik Sayfa 174-175 Cevapları

3.1. Üçgende Açı ve Kenarlarla İlgili Özellikler

Konuya Başlarken

1. Hangi açıların ölçülerinin eşit olduğunu gerekçeleriyle belirtiniz.

Cevap: Şekilde verilen DE // KL ve DE, üçgenin bir paralel kenar oluşturmasına neden olur. Paralellik nedeniyle:

• e = c → İç ters açılardır.
• d = b → İç ters açılardır. Bu nedenle e ve c, d ve b açıları birbirine eşittir.

2. Üçgenin iç açılarının ölçüleri toplamı ile doğru açı arasındaki ilişkiden hareketle ulaştığınız sonucu açıklayınız.

Üçgenin iç açılarının toplamı: a + b + c = 180°

Bu, bir doğru açı oluşturur. Şekilde a, b, c açıları bir doğru üzerindeki açılar gibi sıralanır ve toplamı 180° eder. Bu, her üçgende iç açılar toplamının sabit olduğunu gösterir.

3. İkinci soruda ulaştığınız sonucun tüm üçgenlere genellenip genellenemeyeceğini açıklayınız.

Cevap: Evet, genellenebilir. Üçgenin iç açılarının toplamı her zaman 180°'dir. Bu durum, üçgenin şekline (dar açılı, dik açılı, geniş açılı) bağlı olmaksızın tüm üçgenler için geçerlidir. Bu kural, geometri teoremlerine dayalıdır.

1. Uygulama Cevapları

Üçgenin İç Açılarının Ölçüleri Toplamı
Aşağıda verilen teoremin ispatına yönelik adımları uygulayınız.
1. Teoremi inceleyiniz.

1. Teorem: Üçgenin iç açılarının ölçüleri toplamı 180°'dir.

İspat için verilenler:

• ABC üçgeni
• İspatlanacak ifade: m(∠A) + m(∠B) + m(∠C) = 180°

2. Teoremin iki paralel doğrunun bir kesenle yaptığı açılar kullanılarak nasıl ispatlanabileceğine ilişkin fikirleriniz:

• Konuya başlarken kısmında gösterildiği gibi, paralel doğruların bir kesenle yaptığı açıları kullanabiliriz.
• Doğru açının 180° olduğunu biliyoruz. İç ters açılar yardımıyla, üçgenin iç açılarının toplamının da 180° olduğunu söyleyebiliriz.

3. İkinci adımda karar verdiğiniz ispat yöntemine uygun olarak gerekli çizimleri yapınız ve açıklamalarınızı yazınız.

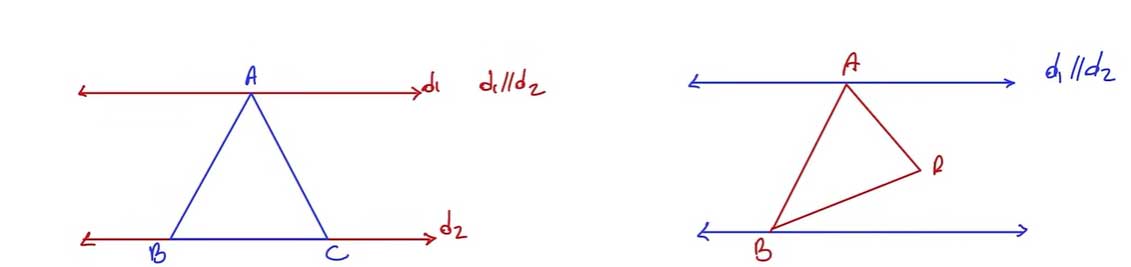
• Şekilde üçgenin tabanına paralel bir doğru çizilir ve bu paralel doğru, üçgenin iki kenarını kesen doğrularla kesişir.
• Paralel doğrunun oluşturduğu açılar, üçgenin iç açılarıyla eşit olan iç ters açılar olarak karşımıza çıkar.
• Bu açıların toplamının bir doğru açıya eşit olduğu, yapılan çizim ve paralellik kuralıyla kanıtlanır.

4. Yaptığınız çizim sonucunda oluşan açılar ile bu açıların ölçüleri arasındaki ilişkiyi açıklayınız.

Paralel doğruya göre oluşan açılar:

• m( DÂB ) = m( ABĈ ) → yöndeş açılar eşittir.
• m( EÂC ) = m( AĈE ) → iç ters açılar eşittir.

Matematiksel ifade:
m(DÂB) = m(ABC)
m(EÂC) = m(ACÊ)

5. Yaptığınız çizim sonucunda oluşan açılar ile üçgenin iç açıları arasındaki ilişkiyi açıklayınız.

Yaptığınız çizimde oluşan açılar ile üçgenin iç açıları arasındaki ilişki:

Paralel doğru üzerindeki açıların her biri üçgenin bir iç açısına karşılık gelir:

• m(DÂB) = m(ABĈ) → üçgenin B iç açısı
• m(EÂC) = m(AĈE) → üçgenin C iç açısı

Matematiksel ifade:
m(DÂB) = m(ABC)
m(EÂC) = m(ACB)

6. Dördüncü ve beşinci adımda elde ettiğiniz ilişkileri kullanarak üçgenin iç açılarının toplamına ilişkin ulaştığınız sonucu yazınız:

Tam açı 180°’dir.
m( D Â B ) + m( B Â C ) + m( C Â F ) = 180°
b + a + c = 180° → üçgenin iç açıları toplamı 180°’dir.

7. Teoremin ispatının tamamlanıp tamamlanmadığına ilişkin fikirlerinizi açıklayınız:

• Teoremin ispatı yapılmıştır.
• Gerekçeleri ve dayanakları paralellik kuralı, iç ters açılar ve doğru açı kavramına dayanarak açıklanmıştır. Ulaşılan sonuçların geçerliliği matematiksel olarak kanıtlanmıştır.