9. Sınıf Matematik 1. Ders Kitabı Sayfa 172-173 Cevapları Meb Yayınları

9. Sınıf Matematik MEB Yayınları Sayfa 182-183 Cevapları

Ön Değerlendirme Cevapları

1. Soru: Verilen geometrik şekilleri numaralandırılmış kavramlarla eşleştirerek doğru harfi kavramın altındaki boşluğa yazınız.

Eşleştirmeler:

1. Dar açı: h (Verilen şekilde açının ölçüsü 90°'den küçüktür.)
2. Geniş açı: g (Şekilde açının ölçüsü 90° ile 180° arasındadır.)
3. Dik açı: c (Açının ölçüsü 90°’dir.)
4. Doğru açı: d (Açının ölçüsü 180°’dir.)
5. Tam açı: a (Açının ölçüsü 360°’dir.)
6. İkizkenar üçgen: f (İki kenarının uzunluğu eşit olan üçgendir.)
7. Eşkenar üçgen: b (Üç kenarının uzunluğu eşit olan üçgendir.)
8. Dik üçgen: e (Bir açısının ölçüsü 90° olan üçgendir.)

2. Soru: Verilen işlem basamaklarını takip ederek boş bırakılan alana uygun çizimi yapınız.

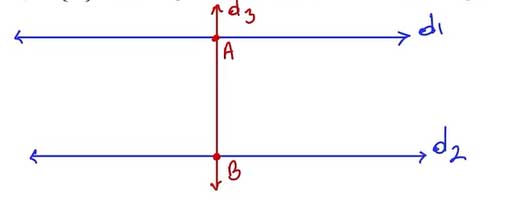
Sonuç: Bir dik doğru ve iki paralel doğru çizilerek, A ve B noktalarının doğrular üzerindeki yerleri belirlenir.

3. Soru: Aşağıda verilen soruları cevaplayınız.

I. Soru: Düzlemde bir d doğrusuna bu doğru üzerinde olmayan bir A noktasından kaç farklı paralel doğru çizilebilir?

Cevap: Bir doğruya, üzerinde bulunmayan bir noktadan yalnızca bir tane paralel doğru çizilebilir. Bu durum, Öklid geometrisinin temel ilkelerinden biridir.

II. Soru: Bir d doğrusu verilmiş olsun. Bu doğru üzerinde olmayan bir A noktasından bu doğruya paralel olmayan iki farklı doğru çizildiğinde oluşan şekil hakkında ne söylenebilir?

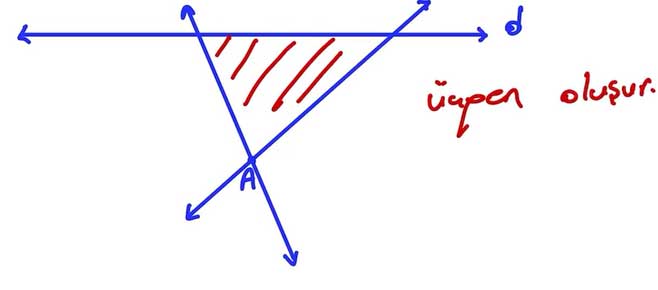
Cevap: A noktasından d doğrusuna paralel olmayan iki farklı doğru çizildiğinde, bu doğrular d ile kesişir ve bir üçgen oluşturur. Üçgenin köşeleri, A noktası ve doğruların kesişim noktaları olur. Bu şekilde geometrik bir şekil ortaya çıkar.

4. Soru: Şekildeki açıların türlerini belirleme

Şekilde verilen açılar için “ters”, “iç ters”, “dış ters”, “yöndeş” ve “karşı durumlu” ifadelerinden uygun olanlarını kullanarak boşluklar doldurulmuştur:

a ile c açıları … ters … açılardır.
b ile d açıları … ters … açılardır.
e ile g açıları … ters … açılardır.
f ile h açıları … ters … açılardır.

d ile f açıları … iç ters … açılardır.
c ile e açıları … iç ters … açılardır.
b ile h açıları … dış ters … açılardır.
a ile g açıları … dış ters … açılardır.

a ile e açıları … yöndeş … açılardır.
b ile f açıları … yöndeş … açılardır.
c ile g açıları … yöndeş … açılardır.
c ile f açıları … karşı durumlu … açılardır.

5. Soru: m(∠BDF) açısını bulma

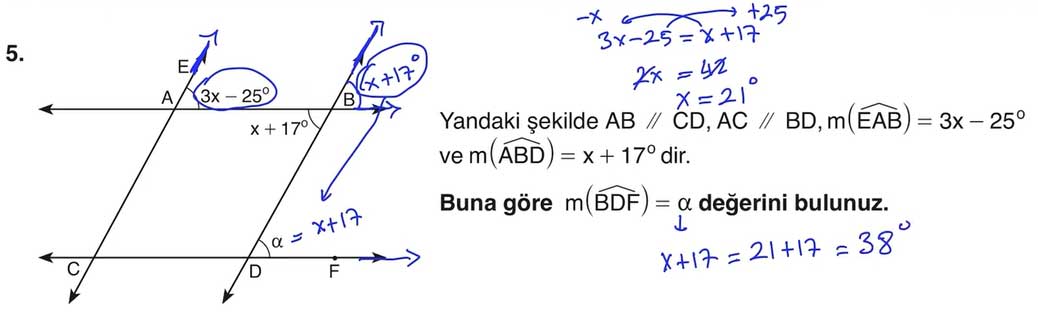
Verilen bilgiler:

• AB // CD, AC // BD
• m(∠EAB) = 3x - 25°
• m(∠ABD) = x + 17°

Çözüm:

m(∠BDF) = α olarak belirlenmiş.
Yöndeş açılar ve paralellik kurallarına göre, 3x - 25 = x + 17 = α.
Denklemi çözerek x'in değerini bulalım:

• 3x - 25 = x + 17
• 2x = 42
• x = 21

Bulduğumuz x değerini yerine koyarak α’yı hesaplayalım:

• α = x + 17
• α = 21 + 17
• α = 38

Sonuç: m(∠BDF) = 38°

6. Soru: Beren x ile gösterilen açının ölçüsünü kaç derece bulmuştur?

Verilen bilgiler:

• m(∠A) = 50°
• m(∠B) = 30°
• Üçgenin iç açılar toplamı = 180°

Çözüm:

x + 30 + 80 = 180
x + 110 = 180
x = 70°

Beren, AC kenarına paralel bir doğru çizdiği için
30° ve 80° açıları yöndeş / iç ters açı olarak üçgenin iç açısına taşınmış olur.

Üçgenin iç açıları toplamı:
30° + 80° + x = 180° → x = 70°

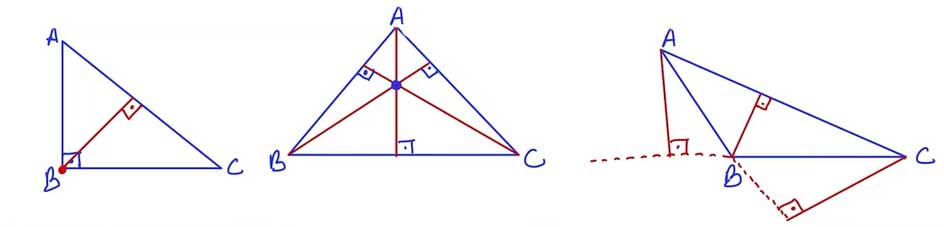
7. Soru: Bir ABC üçgeni ve bu üçgenin kenarlarına ait yükseklikleri çiziniz. Çizdiğiniz yüksekliklerin kesişim noktasının

I. ABC üçgeninin iç bölgesinde,
II. ABC üçgeninin bir köşesi üzerinde,
III. ABC üçgeninin dış bölgesinde
olması durumunda ABC üçgeninin açıları bakımından hangi tür üçgen sınıfına gireceğini açıklayınız.

I. Yüksekliklerin kesim noktası üçgenin iç bölgesindeyse → ABC üçgeni dar açılı üçgendir.

II. Yüksekliklerin kesim noktası üçgenin bir köşesi üzerindeyse → ABC üçgeni dik açılı üçgendir.

III. Yüksekliklerin kesim noktası üçgenin dış bölgesindeyse → ABC üçgeni geniş açılı üçgendir.