9. Sınıf Matematik 1. Ders Kitabı Sayfa 116-119 Cevapları Meb Yayınları

Alıştırmalar – Sayfa 116 (Soru ve Cevaplar)
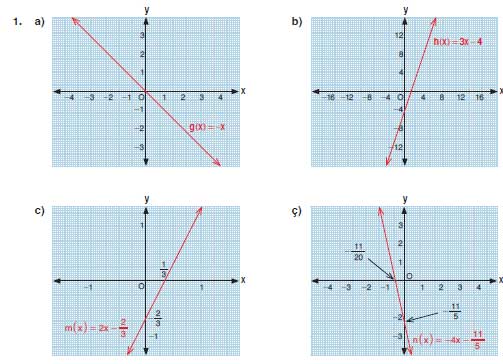
1) Aşağıdaki cebirsel gösterimi verilen, gerçek sayılarda tanımlı fonksiyonların grafiğini; f(x)=x doğrusal referans fonksiyonuna uygun dönüşümleri açıklayarak çiziniz.
a) g(x) = −x
- Eğim: −1 (f(x)=x’in x-ekseni’ne göre yansıması).
- y-kesişimi: 0
- x-kesişimi: 0
- Artış/Azalış: Azalan (R’nin tamamında).
- Çizim ipucu: (−2,2), (−1,1), (0,0), (1,−1), (2,−2) noktalarını birleştir.
b) h(x) = 3x − 4
- Eğim: 3 (f(x)=x doğrusunun dikleştirilmiş hâli; 3 kat dik).
- y-kesişimi: −4 (4 birim aşağı ötelenmiş).
- x-kesişimi: h(x)=0 ⇒ x=4/3.
- Artış/Azalış: Artan.
- Çizim ipucu: y-kesişimi (0,−4); 1 birim sağa gidince 3 birim yukarı (1,−1); x-kesişimi (4/3,0).
c) m(x) = 2x − 2/3
- Eğim: 2 (f(x)=x’in 2 kat dik hâli).
- y-kesişimi: −2/3 (yaklaşık −0,67; aşağı öteleme).
- x-kesişimi: m(x)=0 ⇒ x=1/3.
- Artış/Azalış: Artan.
- Çizim ipucu: (0,−2/3) ve (1, 4/3) noktalarını kullan.
ç) n(x) = −4x − 11/5
- Eğim: −4 (g(x)=−x’in 4 kat dik hâli; x-ekseni’ne göre yansıma + dikleştirme).
- y-kesişimi: −11/5 (−2,2).
- x-kesişimi: n(x)=0 ⇒ x= −11/20 (≈ −0,55).
- Artış/Azalış: Azalan.
- Çizim ipucu: (0,−11/5) ve (1, −31/5) noktaları doğruyu belirler.
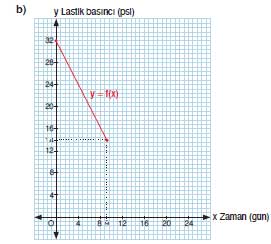
2. Arzu Hanım, aracının lastiğini 32 psi basınçta şişirmiştir. Sonrasında lastik basıncının her gün 2 psi düştüğünü fark etmiştir. Basınç 32 psi’den 14 psi’ye düşene kadar lastiğe müdahale etmemiştir.
a) Zamana (gün) bağlı lastik basıncını (psi) ifade eden doğrusal fonksiyonun tanım ve görüntü kümelerini bularak cebirsel gösterimini yazınız.
Çözüm:
Başlangıç Değeri: Lastik basıncı başlangıçta 32 psi’dir.
Eğim (m): Her gün 2 psi azaldığı için m=−2
Fonksiyonun Genel Denklemi: f(t)=−2t+32
Tanım Kümesi:
Basınç 32 psi’den 14 psi’ye düşünceye kadar geçen süreyi hesaplayalım:
32−14=18 (toplam azalma)
18/2=9 (9 gün)
Tanım kümesi: t∈[0,9]
Görüntü Kümesi: Lastik basıncı başlangıçta 32, sonunda 14’tür. Bu nedenle: f(t)∈[14,32]
Cebirsel Gösterim:
Fonksiyon: f(t)=−2t+32 t∈ [0,9]
Görüntü kümesi: f(t)∈[14,32]
b) Cebirsel gösterimini yazdığınız fonksiyonun grafiğini f(x)=x fonksiyonunun grafiğine uygun dönüşümler yaparak çiziniz.
- Eğim: −2 → x-ekseni’ne göre yansıma (negatif) ve 2 kat dikleştirme.
- y-kesişimi: 32 → 32 birim yukarı öteleme.
- Ana noktalar: (0,32), (4,24), (8,16), (9,14). Bu noktaları birleştirerek azalan doğruyu çizin.
Alıştırmalar – Sayfa 117 Cevapları
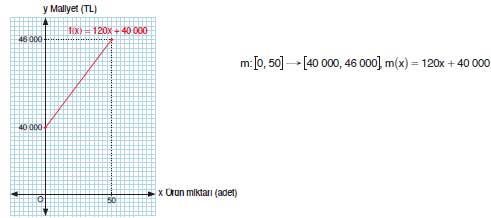
3) Okul çantası üreten bir şirketin günlük sabit üretim maliyeti 40 000 TL’dir. Her bir okul çantasının üretim maliyeti ise 120 TL’dir. x adet okul çantası üretildiğinde günlük toplam maliyeti, [0,50] aralığında tanımlı m doğrusal fonksiyonu ile ifade ediniz. m fonksiyonunun cebirsel ifadesini ve grafik temsilini yazınız.
Cevap: Toplam maliyet, sabit maliyet + üretim miktarı × birim maliyet formülüyle hesaplanır.
Bu durumda:
m(x) = 120x + 40 000
- Tanım Kümesi: [0, 50]
- Görüntü Kümesi: [40 000, 46 000]
- Yorum: 0 ürün üretildiğinde bile fabrikanın sabit gideri 40 000 TL’dir. Her ürün başına maliyet 120 TL olduğundan, üretim arttıkça toplam maliyet doğrusal olarak artar.
- Grafik: y-eksenini 40 000 noktasında keser, x arttıkça doğrusal biçimde yükselir.
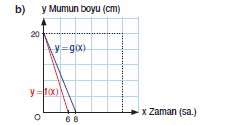
4) 20 cm boyundaki iki mum aynı anda yakılıyor. Mumların biri 6 saatte, diğeri 8 saatte tamamen eriyor. Zaman (saat) değişkenine bağlı mum boyunu (cm) veren f ve g doğrusal fonksiyonlarına göre aşağıdaki soruları cevaplayınız.
a) f ve g fonksiyonlarının cebirsel temsilleri
Cevap: Birinci mum 6 saatte 20 cm yanar → her saatte 20/6 = 10/3 cm azalır.
İkinci mum 8 saatte 20 cm yanar → her saatte 20/8 = 5/2 cm azalır.
Buna göre fonksiyonlar:
- f(x) = 20 − (10/3)x
- g(x) = 20 − (5/2)x
- f: [0, 6] → [0, 20]
- g: [0, 8] → [0, 20]
b) f ve g fonksiyonlarının grafiklerini aynı koordinat sisteminde gösteriniz.
Cevap: Her iki fonksiyonun grafiği (0, 20) noktasından başlar.
- f fonksiyonu, 6. saatte 0’a ulaşır ve daha diktir (daha hızlı yanma).
- g fonksiyonu, 8. saatte 0’a ulaşır ve daha yataydır (daha yavaş yanma).
Grafiklerde doğrular negatif eğimli olup her ikisi de azalan fonksiyonlardır.
c) Fonksiyonların eğimlerini bularak bağlamsal anlamlarını açıklayınız.
Eğim (m) f için −10/3, g için −5/2’dir.
Eğimler negatif olduğundan her iki mumun boyu zamanla azalır.
Eğimin mutlak değeri büyük olan (f) daha hızlı yanar.
ç) Fonksiyonların eksenleri kestiği noktaları bularak bağlamsal anlamlarını açıklayınız.
y-eksenini kestikleri nokta: (0, 20) → başlangıçta mumların boyu 20 cm’dir.
x-eksenini kestikleri noktalar:
- f için (6, 0) → mumun 6 saatte tamamen yanacağını gösterir.
- g için (8, 0) → mumun 8 saatte tamamen yanacağını gösterir.
5) m(x) = −(1/2)x + 1/3 ve n(x) = 6x fonksiyonları veriliyor.
a) f(x) = x doğrusal referans fonksiyonundan yararlanarak m ve n fonksiyonlarının grafiklerini çiziniz.
- m(x): f(x)=x doğrusunun x-ekseni’ne göre yansıması, 1/2 oranında daraltılması ve yukarı 1/3 birim ötelenmesiyle elde edilir.
- n(x): f(x)=x doğrusunun 6 kat dikleştirilmiş hâlidir.
Grafikte m(x) azalan, n(x) ise artan bir doğru şeklindedir.
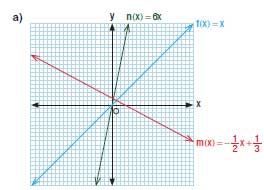
b) Çizdiğiniz grafiklerden yararlanarak m ve n fonksiyonlarının eğimlerini bulunuz. Bulduğunuz eğim değerlerini f fonksiyonunun eğimiyle karşılaştırınız.
- m fonksiyonu eğimi: −1/2 → negatif, dolayısıyla azalan.
- n fonksiyonu eğimi: 6 → pozitif, dolayısıyla artan.
- f fonksiyonu eğimi: 1’dir.
Sonuç olarak, n fonksiyonu f’ye göre daha dik, m fonksiyonu ise ters yönde ve daha yatıktır.
c) m ve n fonksiyonlarının grafikleri f doğrusal referans fonksiyonunun grafiğine hangi dönüşümler uygulanarak elde edilir?
m(x) = −(1/2)f(x) + 1/3
- x-ekseni’ne göre yansıtılmıştır.
- Dikeyde 1/2 oranında daraltılmıştır.
- Yukarı doğru 1/3 birim ötelenmiştir.
n(x) = 6f(x)
-
Dikeyde 6 kat genişletilmiş, herhangi bir öteleme uygulanmamıştır.
Alıştırmalar – Sayfa 118 Cevapları
5-ç) m ve n fonksiyonlarının sıfırlarını, y eksenini kestikleri noktaları, maksimum ve minimum değerlerini bulunuz.
m(x) = −1/2x + 1/3
→ m(x) = 0 ⇒ −1/2x + 1/3 = 0 ⇒ x = 2/3
→ y-eksenini (0, 1/3) noktasında keser.
n(x) = 6x
→ n(x) = 0 ⇒ x = 0
→ y-eksenini (0, 0) noktasında keser.
Her iki fonksiyon doğrusal olduğundan maksimum veya minimum değerleri yoktur.
| Fonksiyon | Sıfır Noktası | y-Eksenini Kestiği Nokta | Maksimum | Minimum |
|---|---|---|---|---|
| m(x) | x = 2/3 | (0, 1/3) | Yok | Yok |
| n(x) | x = 0 | (0, 0) | Yok | Yok |
5-d) Fonksiyonların artanlık ve azalanlık durumlarını inceleyiniz.
- m(x) = −1/2x + 1/3 → eğim < 0 ⇒ azalan fonksiyon
- n(x) = 6x → eğim > 0 ⇒ artan fonksiyon
Sonuç: m doğrusu x arttıkça aşağı yönlü, n doğrusu yukarı yönlü hareket eder.
5-e) Fonksiyonların bire bir olup olmadıklarını belirleyiniz.
Cevap: Her iki fonksiyon da doğrusal ve eğimleri 0’dan farklı olduğundan tanımlı oldukları tüm aralıklarda bire birdir.
Yani farklı x değerleri, farklı y değerleri verir.
5-f) Fonksiyonların artanlığı-azalanlığı ve bire birliği sonuçlarını cebirsel olarak doğrulayınız.
Cevap: m(x) = −1/2x + 1/3 fonksiyonu için:
x₁ < x₂ olduğunda,
−1/2x₁ > −1/2x₂ ⇒ m(x₁) > m(x₂)
Bu nedenle m(x) azalan fonksiyondur.
Ayrıca x₁ ≠ x₂ ⇒ −1/2x₁ + 1/3 ≠ −1/2x₂ + 1/3 ⇒ m(x₁) ≠ m(x₂)
Bu nedenle m(x) bire birdir.
n(x) = 6x fonksiyonu için:
x₁ < x₂ ⇒ 6x₁ < 6x₂ ⇒ n(x₁) < n(x₂)
Bu nedenle n(x) artan fonksiyondur.
Ayrıca x₁ ≠ x₂ ⇒ 6x₁ ≠ 6x₂ ⇒ n(x₁) ≠ n(x₂)
Bu nedenle n(x) bire birdir.
6. Soru
Bir çözeltideki maddenin derişim miktarını veren fonksiyon:
f:[0,40] → [0,8], f(x)=−0,2x+8
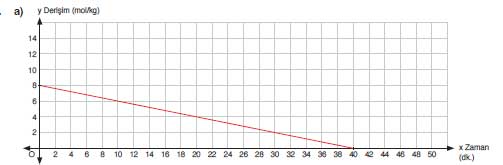
6-a) f fonksiyonunun grafiğini çiziniz.
Cevap: Başlıca noktalar:
- (0, 8) → başlangıç derişimi
- (20, 4) → 20. dakikada yarı miktar
- (40, 0) → 40. dakikada sıfır
Grafik orijine doğru inen, negatif eğimli bir doğru oluşturur.
Fonksiyon azalan bir doğrusal grafiktir.
6-b) İlacın vücuttaki derişim miktarının zamana bağlı değişimini f fonksiyonunun grafiğiyle açıklayınız.
Cevap: Zaman (x) arttıkça derişim (y) doğrusal biçimde azalır.
Her dakika derişim miktarı 0,2 mol/kg azalır.
Başlangıçta 8 mol/kg olan ilaç, 20. dakikada 4’e, 40. dakikada 0’a düşer.
Bu da ilacın etkisinin zamanla düzenli biçimde azaldığını gösterir.
6-c) İlacın vücuttaki derişim miktarı sıfır olduğunda ilacın etkisi tamamen kaybolmaktadır.
İlacın etkisinin tamamen kaybolması için gereken zamanı bulunuz.
Cevap:
f(x) = 0 ⇒ −0,2x + 8 = 0
⇒ x = 40
Sonuç: İlacın etkisi 40. dakikada tamamen kaybolur.
Alıştırmalar – Sayfa 119 Cevapları
7. Soru – Doğrusal Fonksiyon
Verilen Bilgiler:
- f fonksiyonunun grafiği, y ekseni boyunca 5 birim yukarı ötelendiğinde g(x) = ax + 3 grafiğini oluşturur.
- f fonksiyonunun sıfırı x = –3 tür.
- f fonksiyonunun maksimum değeri 2, minimum değeri –4 tür.
a) f fonksiyonunun cebirsel ifadesi
Sıfır noktası x = –3 olduğuna göre f(–3) = 0.
g(x) = ax + 3 grafiği, f’nin y ekseni boyunca 5 birim yukarı ötelenmiş hâlidir.
Yani g(x) = f(x) + 5 ⇒ f(x) = g(x) – 5
g(x) = ax + 3 yerine yazılırsa:
f(x) = ax + 3 – 5
f(x) = ax – 2
Sıfır noktası x = –3 için f(–3) = 0 ⇒ a(–3) – 2 = 0 ⇒ a = –2/3
Cevap: f(x) = –2/3x – 2, tanım aralığı [–6, 3], değer aralığı [–4, 2].
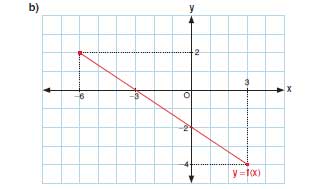
b) f fonksiyonunun grafiği
Negatif eğimli bir doğrudur.
- x = –6 için f(–6) = 2
- x = 3 için f(3) = –4
Grafik bu iki noktayı birleştiren azalan bir doğrudur.
c) f fonksiyonunun artan ya da azalanlığı
Eğim (m) = –2/3 < 0 olduğundan f fonksiyonu azalandır.
ç) f fonksiyonunun işareti
- (–6, –3) aralığında f(x) > 0’dır.
- [–3, 3] aralığında f(x) ≤ 0’dır.
Yani x = –3 noktasında sıfır, sonrasında negatif değerler alır.
8. Soru – Uçak Yüksekliği Fonksiyonları (f, g, h)
Grafikten uçuşun kalkış, seyir ve iniş evrelerindeki eğimler hesaplanır.
a) Yükseklik değişim oranları
- Kalkış süreci: 5/6 m/sn
- Seyir süreci: 0 m/sn (sabit yükseklik)
- İniş süreci: –5/8 m/sn
b) İniş süresinin kalkıştan uzun olmasının nedeni
Kalkış eğimi 5/6, iniş eğimi –5/8’dir.
Eğimlerin mutlak değerleri farklı olduğundan, kalkış daha hızlı (daha dik), iniş daha yavaş (daha yatay) gerçekleşir.
Bu nedenle iniş süresi kalkış süresinden uzundur.







Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.