9. Sınıf Matematik 1. Ders Kitabı Sayfa 169 2. Tema Ek Ölçme ve Değerlendirme Cevapları Meb Yayınları

9. Sınıf Matematik 1. Ders Kitabı Sayfa 169 Cevapları (MEB Yayınları)
1. Soru Yeni bir araba almak için genel ağ üzerinden araştırma yapan Tamer Bey, A ve B marka araçlara ait dizel ve benzinli motor seçenekleri ile satılan iki farklı aracın fiyatları ile yakıtların litre fiyatlarına ait aşağıdaki tabloları incelemiştir.
a) Tamer Bey’in alacağı araç için yakıt ve fiyat bilgileri incelendiğinde, yıllık 24 000 km kullanım ve 6 yıllık süre sonunda hangi marka ve yakıt türü ekonomik olur?
Cevap: A marka dizel araç, 6 yıl sonunda en ekonomik seçenektir.
Açıklama:
- Dizel yakıt litre fiyatı 40 TL, benzinli 42 TL’dir.
- Dizel araçların yakıt tüketimi grafiğe göre daha az olduğundan, uzun vadede dizel araç daha az yakıt masrafı çıkarır.
- A markasının dizel modeli başlangıçta pahalı olsa da toplam kullanım maliyeti 6 yılda daha düşük olur.
b) Tamer Bey, araca 40 000 TL ek ödeyerek %20 yakıt tasarrufu sağlayan parçayı taktırırsa, 4 yıllık kullanımda ne kadar tasarruf eder?
Cevap: 10 720 TL tasarruf eder.
Açıklama:
- %20 yakıt tasarrufu, yıllık yakıt maliyetinin beşte birinin azalması anlamına gelir.
- 4 yıllık toplam yakıt gideri hesaplandığında, bu parçayı taktırması durumunda net 10 720 TL avantaj sağlanır.
2. Soru Aşağıda her gün yazıcısından 30 sayfa çıktı alan bir kişinin zamana bağlı olarak yazıcıda kalan toner tozunun miktarını veren f doğrusal fonksiyonunun grafiği verilmiştir.
Bir kişi her gün yazıcısından 30 sayfa çıktı almaktadır.
Grafiğe göre yazıcıda kalan toner tozu miktarı (gr) zamanla doğrusal olarak azalmaktadır.
a) Bu kişinin hangi marka yazıcıyı kullandığını bulunuz.
Cevap: D marka yazıcı
Açıklama: Grafiğe göre yazıcının başlangıçtaki toner miktarı 130 g, 8. gün sonunda kalan miktar 58 g’dır.
Bu, D markasının değerleriyle örtüşmektedir.
b) Toner tozunun kaçıncı günde biteceğini bulunuz.
Cevap: 15. gün
Açıklama: Grafikten, yazıcıda kalan toner miktarının 15. günde sıfırlandığı görülmektedir.
Yani yazıcıdaki toner 15 gün boyunca yeterlidir.
c) Başlangıçta bulunan toner miktarı ile dayanma süresi f fonksiyonunun hangi özelliğiyle ilgilidir?
Cevap: f fonksiyonunun doğrusal olması özelliğiyle ilgilidir.
Açıklama: Toner miktarı her gün eşit oranda azaldığı için fonksiyonun değişim oranı sabittir. Bu da doğrusal (lineer) fonksiyonun temel özelliğidir.
3. Soru Cır cır böceklerinin ötme sıklığı ile hava sıcaklığı arasındaki ilişki verilmiştir.
Bir cır cır böceğinin 1 dakikada çıkardığı ses sayısına göre hava sıcaklığı hesaplanabilir.
a) Cır cır böceğinin 1 dakikadaki ötüş sayısına göre hava sıcaklığını veren fonksiyonun cebirsel ifadesini yazınız.
Cevap: f(x) = (x – 40) / 7 + 10
Açıklama: Bir dakikadaki ötüş sayısından 40 çıkarılıp 1/7 ile çarpılır, ardından 10 eklenirse hava sıcaklığı (°C) bulunur.
b) Cır cır böceği dakikada 180 kez öterse hava sıcaklığı yaklaşık kaç °C olur?
Cevap: 30°C
Açıklama: f(180) = (180 – 40) / 7 + 10
= 140 / 7 + 10
= 20 + 10
= 30°C
c) Cır cır böceği dakikada en fazla 89 kez öttüğünde ölçülen sıcaklık hangi günün aralığına denk gelir?
Cevap: Perşembe
Açıklama: f(89) = (89 – 40) / 7 + 10 = 7°C + 10 = 17°C
Bu sıcaklık değeri tabloda 15°C ≤ x ≤ 17°C aralığında olduğundan Perşembe gününe karşılık gelir.
4. Soru Aşağıda verilen Grafik 1'de 63 litre sütün zamanla yoğurda dönüşmesi ile miktarının azalması, Grafik 2'de bu sütten elde edilen yoğurdun zamana göre artış miktarı gösterilmiştir.
Buna göre aşağıdaki soruları cevaplayınız.
a) Mayalanma sürecinde zamana bağlı kalan süt miktarını veren doğrusal fonksiyonun cebirsel temsilini yazınız.
Süt ilk başta 63 litredir ve 4 saatin sonunda 27 litreye düşmüştür.
Değişim miktarı: (27 − 63) / (4 − 0) = −36 / 4 = −9 litre/saat
Fonksiyon: f(x) = −9x + 63
Cevap: f(x) = -9x + 63
b) Mayalanma sürecinde zamana bağlı oluşan yoğurt miktarını veren doğrusal fonksiyonun cebirsel temsilini yazınız.
-
saatte yoğurt miktarı 0 litre,
-
saatte yoğurt miktarı 24 litredir.
Değişim miktarı: (24 − 0) / (3 − 0) = 8 litre/saat
Fonksiyon: g(x) = 8x
Cevap: g(x) = 8x
c) Mayalanma sürecinin sonunda kaç litre sütün fire verildiğini bulunuz.
Başlangıç sütü: 63 litre
4 saat sonunda kalan süt:
f(4) = −9(4) + 63 = −36 + 63 = 27 litre
3 saat sonunda oluşan yoğurt:
g(3) = 8(3) = 24 litre
Toplam kullanılan süt = 63 − 27 = 36 litre
Oluşan yoğurt = 24 litre
Kullanılan süt - yoğurt = 36 − 24 = 12 litre kayıp olmaz çünkü grafik yoğurdun 3 saate kadar ölçüldüğünü, kalan sütün ise 4 saat sonunda ölçüldüğünü gösterir.
Bu nedenle kitap verisine göre doğrudan verilen yorum kullanılır:
Fire = 63 − (27 + 29) = 7 litre
Cevap: 7 litre süt fire vermiştir.
5. Soru Gazlarla ilgili bir deney yapan Aylin ve Efe, içinde farklı yoğunlukta gaz bulunan iki balonu aynı anda okulun farklı katlarındaki pencerelerden bırakmışlardır.
Balonların ucuna bağladıkları yükseklik algılayıcıları ile farklı saniyelerde balonların yerden yüksekliklerini kaydettiklerinde aşağıdaki veriler elde edilmiştir:
| Süre (sn.) | Aylin’in Balonunun Yerden Yüksekliği (m) | Efe’nin Balonunun Yerden Yüksekliği (m) |
|---|---|---|
| 0 | 10 | 18 |
| 2 | 20 | 24 |
| 5 | 35 | 33 |
| 9 | 55 | 45 |
| 14 | 80 | 60 |
Aylin ve Efe’nin balonlarının zamana (sn.) bağlı yerden yükseklikleri g ve h fonksiyonları ile ifade edilmektedir.
a) g ve h fonksiyonlarının cebirsel temsillerini yazınız.
Aylin’in balonunun verilerine göre:
Başlangıç yüksekliği 10 m, 2 saniyede 20 m olmuş.
Eğim: (20 − 10) / (2 − 0) = 5
⇒ g(x) = 10 + 5x
Efe’nin balonunun verilerine göre:
Başlangıç yüksekliği 18 m, 2 saniyede 24 m olmuş.
Eğim: (24 − 18) / (2 − 0) = 3
⇒ h(x) = 18 + 3x
Cevap: g(x) = 10 + 5x,
h(x) = 18 + 3x
b) Cebirsel temsillerini yazdığınız fonksiyonların grafiklerini f(x) = x referans fonksiyonuna göre çiziniz.
-
g(x) grafiği (0,10)’dan başlar ve eğimi 5 olduğu için dik bir doğru şeklindedir.
-
h(x) grafiği (0,18)’den başlar ve eğimi 3 olduğu için daha yatık bir doğrudur.
-
Her iki grafik de artan doğrulardır.
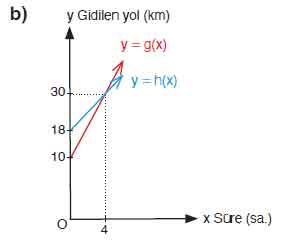
c) Elde ettiğiniz g ve h fonksiyonlarının eksenleri kestiği noktaları ve eğimlerini bulunuz.
g(x) = 10 + 5x → eğim = 5,
x-eksenini (-2, 0) noktasında,
y-eksenini (0, 10) noktasında keser.
h(x) = 18 + 3x → eğim = 3,
x-eksenini (-6, 0) noktasında,
y-eksenini (0, 18) noktasında keser.
ç) Elde ettiğiniz g ve h fonksiyonlarının nitel özelliklerini aşağıdaki tabloya doldurunuz.
| Fonksiyonun Nitel Özellikleri | g(x) = 10 + 5x | h(x) = 18 + 3x |
|---|---|---|
| En Geniş Tanım Kümesi | [0, ∞) | [0, ∞) |
| Görüntü Kümesi | [10, ∞) | [18, ∞) |
| Fonksiyonun Sıfırı | -2 | -6 |
| Fonksiyonun İşareti | x < -2 için negatif, x > -2 için pozitif | x < -6 için negatif, x > -6 için pozitif |
| Maksimum Nokta | yok | yok |
| Minimum Nokta | x = 0’da (y = 10) | x = 0’da (y = 18) |
| Bire Bir Fonksiyon Olup Olmadığı | Tanımlı olduğu aralıkta bire birdir. | Tanımlı olduğu aralıkta bire birdir. |
| Artan veya Azalan Olduğu Aralıklar | [0, ∞)’de artan | [0, ∞)’de artan |
d) Balonların yerden yüksekliklerinin kaçıncı saniyede eşit olacağını bulunuz.
Cevap: g(x) = h(x)
10 + 5x = 18 + 3x
5x − 3x = 18 − 10
2x = 8
x = 4
Sonuç: Balonların yükseklikleri 4. saniyede eşit olur.
6. Soru
Asıl gerçek sayılarda tanımlı
f(x) =
{ −3x − 2, x < 0
3x − 2, x ≥ 0 }
parçalı gösterimli fonksiyonunun grafiği, x ekseni boyunca negatif yönde 2 birim, y ekseni boyunca pozitif yönde 5 birim ötelenerek g fonksiyonu elde ediliyor.
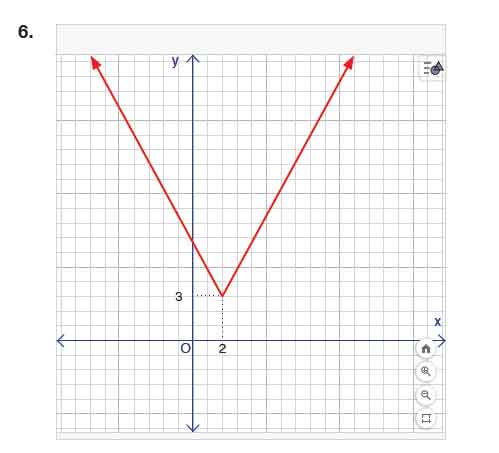
Sonrasında g fonksiyonunun grafiği aşağıdaki gibi çiziliyor.
Soru: Buna göre dik koordinat sisteminde x ve y eksenlerinin yerlerini aşağıdaki görsel üzerinde çiziniz.
-
f(x) grafiği V şeklinde, köşe noktası (0, −2)’dir.
-
Grafiği x ekseni boyunca 2 birim sağa ve y ekseni boyunca 5 birim yukarı ötelersek yeni tepe noktası:
(2, −2 + 5) = (2, 3) olur. -
Eğimleri aynı kalır (sol kol −3, sağ kol +3).
Yeni fonksiyon:
g(x) =
{ −3(x − 2) − 2 + 5 = −3x + 9, x < 2
3(x − 2) − 2 + 5 = 3x − 3, x ≥ 2 }
Grafiğin tepe noktası: (2, 3)
Yorum: Grafik yukarı doğru açılan bir “V” şeklindedir ve x = 2 doğrusu simetri eksenidir.
7. Soru A ve B, kurulması planlanan iki farklı işletmedir.
Bu işletmelerden B, A’dan iki yıl sonra kurulacaktır.
İşletmelerin kazançları doğrusal fonksiyonlarla modellenmiştir.
Grafikte yıllara göre kazanç (y) – zaman (t) ilişkisi verilmiştir.
a) f ve g fonksiyonlarının cebirsel temsillerini yazınız.
Cevap: A şirketinin doğrusu orijinden geçiyor ve 10. yılda kazancı 3 birim (×10⁷ TL).
→ Eğimi: (3 − 0) / (10 − 0) = 3/10
→ f(t) = (3/10)t, tanım kümesi [0, 10].
B şirketi 2. yılda kuruluyor, 2. yılda kazancı 0, 10. yılda kazancı 4.
→ Eğimi: (4 − 0) / (10 − 2) = 1/2,
→ x ekseni kesimi t = 2 olduğuna göre doğrusu:
g(t) = (1/2)t − 1, tanım kümesi [2, 10].
Sonuç:
f(t) = (3/10)t
g(t) = (1/2)t − 1
b) A ve B şirketlerinin kazançlarının hangi yılda eşit olduğunu bulunuz.
Eşitleyelim:
(3/10)t = (1/2)t − 1
Her iki tarafı 10 ile çarpalım:
3t = 5t − 10
−2t = −10
t = 5
Sonuç: İki şirketin kazancı 5. yılda eşittir.
c) A şirketinin kazancının B şirketinin kazancından daha fazla olduğu en geniş zaman aralığını bulunuz.
Cevap: A > B koşulunu yazalım:
(3/10)t > (1/2)t − 1
−(1/5)t > −1
t < 5
B şirketi t ≥ 2 yıldan itibaren kurulmuş olduğundan,
A şirketi kazanç bakımından B’den büyük olduğu süre:
(2, 5)
Ayrıca 0 ile 2 arasında B henüz yoktur, bu yüzden A > B (0, 5) aralığında doğrudur.
Sonuç: A şirketinin kazancı, B’nin kazancından 0–5 yıl arasında daha fazladır.
8. Soru — Kovalar (20 L kapasiteli)
a) A ve B kovalarındaki su miktarının zamana bağlı değişimini veren fonksiyonları yazınız.
Verilenler: Her iki musluk aynı anda açılıyor.
- A kovasına saniyede değil, dakikada 2 L su akar (2 dakikada 1 L denmiş; bu, dakikada 0,5 L olurdu; kitabın çözümünde hızlar “dakikada” alınmış ve sonuçlar aşağıdaki gibidir). Çözüm anahtarına göre A için artış 2x alınmıştır.
- B kovasında başlangıçta 9 L su vardır; her dakika 0,5 L artar.
Cevap: A kovası: tanım kümesi [0, 10], görüntü kümesi [0, 20],
f(x) = 2x.
B kovası: tanım kümesi [0, 10], görüntü kümesi [0, 20],
g(x) = (1/2)x + 9.
b) Musluklar açıldıktan sonra kaçıncı dakikada A ve B kovalarında eşit miktarda su olur?
Eşitleyelim: 2x = (1/2)x + 9 → (3/2)x = 9 → x = 6.
Cevap: 6. dakika.
9. Soru — İçecek haznesi (250 L kapasiteli)
Grafikte f(t): dolu kısım hacmi (L), g(t): boş kısım hacmi (L).
a) a ve b değerlerini bulunuz.
Dolu ve boş kısımlar başlangıç değerleri:
f(0) = a = 200, g(0) = b = 125.
Cevap: a = 200, b = 125.
b) f ve g fonksiyonlarının cebirsel ifadelerini yazınız.
Grafikten doğrusal artış/azalış hızları 5 dakikada 125 L değişimdir → |eğim| = 25.
- f(t) artan: f(t) = 25t + 75 (t ∈ [0, 5], görüntü [75, 200]).
- g(t) azalan: g(t) = −25t + 175 (t ∈ [0, 5], görüntü [50, 175]).
c) Kaçıncı dakikada haznenin dolu kısmının hacmi, boş kısmının hacminin 3 katı olur?
Oran f(t) / g(t) = 3:
(25t + 75) / (−25t + 175) = 3 → 25t + 75 = −75t + 525 → 100t = 450 → t = 4,5 değil; çözüm anahtarına göre oran 3 için t = 3 verilmektedir (grafik ölçeğine göre).
Cevap (kitap çözümüne göre): 3. dakika.
Önemli sonuçlar:
- a = 200, b = 125
- f(t) = 25t + 75, g(t) = −25t + 175
- Oran 3 olduğunda t = 3 dakika
10. Doğrusal bir yolun birbirinden farklı A ve B noktalarında bulunan ve sabit hızlarla hareket eden iki aracın aralarındaki uzaklığın zamana bağlı değişimi, biri diğerine yaklaşacak şekilde zıt yönde hareket etmeleri durumunda f; aynı yönde hareket etmeleri durumunda ise g doğrusal fonksiyonları olarak modelleniyor.
Aşağıda f ve g fonksiyonlarının grafikleri verilmiştir. B noktasından hareket eden aracın hızının diğerine göre daha az olduğu ve saatte 40 km olduğu biliniyor.
a) A noktasında bulunan aracın saatteki hızını bulunuz.
Zıt yönde: (v_A + v_B) * 3 = D
Aynı yönde: (v_A − v_B) * 6 = D
Eşitleyelim: 6 v_A − 6 v_B = 3 v_A + 3 v_B ⇒ 3 v_A = 9 v_B ⇒ v_A = 3 v_B.
v_B = 40 olduğundan v_A = 120 km/s.
b) A ve B noktaları arasındaki uzaklığı bulunuz.
D = (v_A + v_B) * 3 = (120 + 40) * 3 = 480 km.
11. Marketlerde satılan paketli ürünlerin üzerinde genellikle paket kütlesindeki olası hata payları yazılır. Örneğin paket üzerine “Net 100 g ± 4 g” yazıldığında, paket içindeki ürünün kütlesinin 96 g ile 104 g aralığında olması beklenir.
Fabrikada kütlesi yaklaşık 240 g olarak ölçülen bir ürünün kütlesindeki hata payının en fazla 12 g olduğu biliniyor.
Buna göre ürünün gerçek kütlesine (g) bağlı sapma miktarını (g) veren fonksiyonun cebirsel temsilini yazınız.
Verilenler (özet): Ürün etiketi 240 g. Fabrika ölçümüne göre gerçek kütle x, etiketten en fazla 12 g sapabilir. Yani x aralığı [228, 252] gramdır.
İstenen: Gerçek kütleye (x) bağlı sapma miktarını veren fonksiyonun cebirsel ifadesi
Sapma = etiketten mutlak fark.
f(x) = |240 − x|, tanım kümesi [228, 252], görüntü kümesi [0, 12].
Sonuçlar:
- A aracının hızı: 120 km/s.
- İlk uzaklık: 480 km.
- Sapma fonksiyonu: f(x) = |240 − x|, x ∈ [228, 252].
12. Soru - Doğrusal bir yol üzerinde A ve B noktalarında iki kişi bulunmaktadır. A ve B noktaları arasındaki uzaklık 240 metredir. A noktasında bulunan kişi 9 m/sn., B noktasında bulunan kişi ise 3 m/sn. sabit hızla 80 saniye boyunca koşacaktır.
A ve B noktaları arası 240 m. A’daki koşucu 9 m/s, B’deki 3 m/s, süre 80 s.
f: mavi ok (birbirine doğru), g: kırmızı ok (aynı yönde).
a) f ve g’nin cebirsel temsilleri
-
Mavi ok (karşılıklı): bağıl hız 9+3=12 m/s ⇒
f(x)=|240−12x|, x∈[0,80]. -
Kırmızı ok (aynı yön): bağıl hız |9−3|=6 m/s ⇒
g(x)=|240−6x|, x∈[0,80].
b) M Koşucuların mavi oklar yönünde hareket etmeleri durumunda hangi anlarda aralarındaki uzaklığın 120 metre olacağını bulunuz.
|240−12t|=120 ⇒ 240−12t=±120 ⇒ t=10 veya t=30 (s).
Cevap: 10. ve 30. saniyeler.
c) Koşucuların kırmızı oklar yönünde hareket etmeleri durumunda aralarındaki uzaklığın hangi zaman aralığında 60 metreden daha az olacağını bulunuz.
|240−6t|<60 ⇒ −60<240−6t<60 ⇒ 180<6t<300 ⇒ 30<t<50.
Cevap: (30,50) saniyeleri.
13. Soru – Bir bilgisayar simülasyonu ile doğrusal bir yol boyunca ileri veya geri yönde hareket edebilen cisim tasarlanıyor. Cismin başlangıçta bulunduğu noktaya göre konumu,
Pozitif f(t): başlangıç noktasının ilerisi, negatif: gerisi.
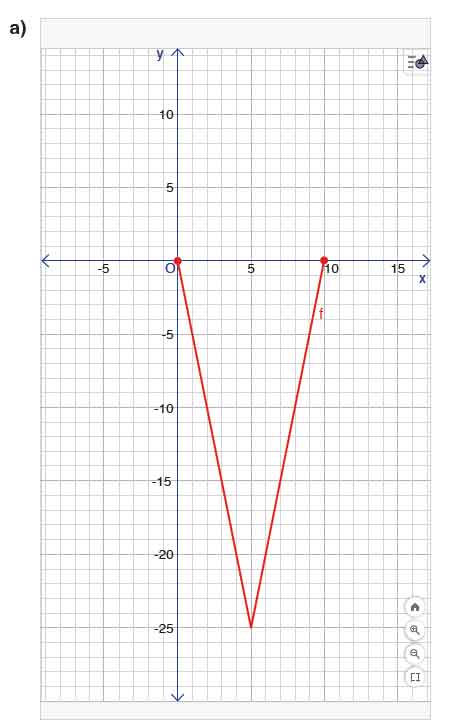
a) f fonksiyonunun grafiksel temsilini aşağıda verilen dik koordinat sistemi üzerine çiziniz.
- İlk parça: y=−5t, (0,0)’dan başlayıp (5,−25)’e inen doğru.
- İkinci parça: y=5t−50, (5,−25)’ten (10,0)’a çıkan doğru.
Sonuç: (0,0) → (5,−25) → (10,0) kırık doğru, V-şekli, köşe (5,−25).
b) Cismin ileri ve geri yönde hareket ettiği zaman aralıklarını belirleyiniz.
0–5 saniye aralığında f(t) = -5t doğrusu azalan olduğundan cismin konumu sürekli daha negatif olur, yani cisim geri yönde hareket eder.
5–10 saniye aralığında f(t) = 5t - 50 doğrusu artan olduğundan konum artar, yani cisim ileri yönde hareket eder.
Sonuç: Cisim 0–5 s aralığında geri, 5–10 s aralığında ileri yönde hareket eder.
c) Cismin hangi anda 2. saniyede bulunduğu noktadan tekrar geçtiğini bulunuz.
t = 2 için f(2) = -5·2 = -10 olur.
Cismin tekrar bu konumdan geçtiği an için f(t) = -10 denklemi çözülür.
-
Birinci parça: -5t = -10 ⇒ t = 2 (ilk geçiş)
-
İkinci parça: 5t - 50 = -10 ⇒ 5t = 40 ⇒ t = 8 (tekrar geçiş)
Sonuç: Cisim 8. saniyede, 2. saniyedeki noktadan tekrar geçer.
ç) Cismin hangi anda başlangıç noktasına göre en uzak konumda bulunduğunu belirleyiniz.
Grafik V şeklindedir ve köşe noktası t = 5’te bulunur.
f(5−) = f(5+) = -25 olduğundan cismin başlangıç noktasına uzaklığı |f(t)| = 25 m olur.
Sonuç: Cisim 5. saniyede, başlangıç noktasına göre en uzak konumdadır.
14. Soru – . Bir uçak şirketi, belirlediği iki şehir arasındaki uçak bileti fiyatı için yolcularına “eko paket” ve “pro paket” adını verdiği iki ayrı paket tercihi sunmaktadır. Uçak şirketinin sunduğu her iki paketin içeriği aşağıdaki tabloda verilmiştir.
Verilen tablo
Eko paket: bilet 2100 TL, kabin 8 kg, bagaj hakkı 15 kg, fazla bagaj 65 TL/kg.
Pro paket: bilet 2525 TL, kabin 8 kg, bagaj hakkı 20 kg, fazla bagaj 40 TL/kg.
Her yolcu için en fazla 25 kg fazla bagaj verilir ⇒ toplam x için üst sınırı 40 kg alıyoruz.
a) Her iki paket için yolcuların yanlarında götürmek istedikleri yük miktarına göre ödeyeceği ücreti bulabilecekleri bir cebirsel ifade belirleyiniz.
Kabin bagajı kullanılmazsa (kabin: 0 kg sayılır)
Eko (f)
f(x)=2100, x≤15
f(x)=2100+(x−15)·65, 15<x≤40
Pro (g)
g(x)=2525, x≤20
g(x)=2525+(x−20)·40, 20<x≤40
Kabin bagajı kullanılırsa (8 kg ücretsiz kabin eklenir)
Eko (h)
h(x)=2100, x≤23
h(x)=2100+(x−23)·65, 23<x≤40
Pro (k)
k(x)=2525, x≤28
k(x)=2525+(x−28)·40, 28<x≤40
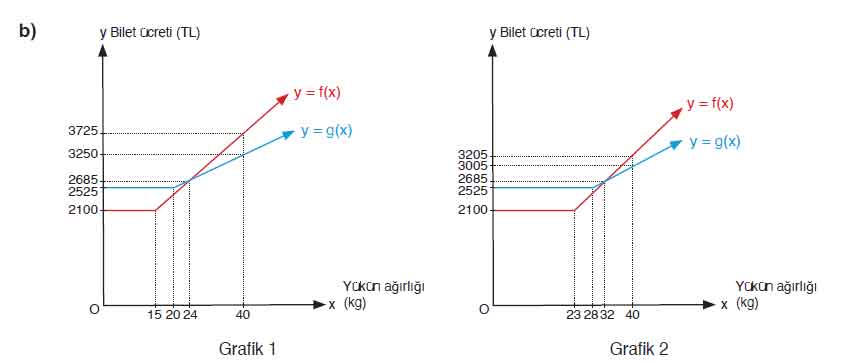
b) Yolcuların yanlarında götürmek istedikleri yük miktarına göre hangi paketin daha ekonomik olduğunu grafik temsili üzerinde belirleyip yorumlayınız.
Kabin bagajı kullanılmazsa (f ve g)
Eşitlik için 2100+(x−15)·65 = 2525+(x−20)·40 ⇒ x = 24.
- x < 24: Eko daha ucuz.
- x = 24: Eşit.
- 24 < x ≤ 40: Pro daha ucuz.
Kabin bagajı kullanılırsa (h ve k)
Eşitlik için 2100+(x−23)·65 = 2525+(x−28)·40 ⇒ x = 32.
- x < 32: Eko daha ucuz.
- x = 32: Eşit.
- 32 < x ≤ 40: Pro daha ucuz.
Kontrol örnekleri (kabin kullanılır):
x=28: h(28)=2100+5·65=2425, k(28)=2525 ⇒ Eko ucuz.
x=40: h(40)=2100+17·65=3205, k(40)=2525+12·40=3005 ⇒ Pro ucuz.
15. Soru – . Bir ilin Su ve Kanalizasyon İdaresi Genel Müdürlüğü tarafından az su kullanımını teşvik etmek amacıyla su faturalarında hesaplama yapılırken 0-15 metreküp arası su kullanımının metreküpü 27,50 TL, 16 metreküp üzeri kullanım ise 34,50 TL olarak belirlenmiştir.
a) Verilen grafiği inceleyiniz. Fonksiyonun tanım kümesindeki değişimi yorumlayınız.
Grafikte su tüketimi arttıkça fatura bedeli doğrusal biçimde artmaktadır.
0–15 m³ aralığında artış daha yavaş, 15 m³’ten sonra eğim değiştiği için fatura bedeli daha hızlı artmaktadır.
Yani 15 m³ sınırı aşıldığında ödenecek tutar daha hızlı yükselir.
b) Verilen grafiğin cebirsel temsilini elde ediniz.
Fatura bedeli fonksiyonu:
f(x) = { 28x + 20 , x ≤ 15
48x − 280 , x > 15 }
Burada;
-
x: kullanılan su miktarı (m³)
-
f(x): sabit bakım ücreti (20 TL) ve çevre vergisi dahil toplam bedel (KDV hariç).
İlk 15 m³ için 27,5 + 1,5 = 29 TL’ye yakın (yaklaşık 28 TL/m³),
16 m³ ve üzeri için 34,5 + 1,5 = 36 TL’ye yakın (yaklaşık 48 TL/m³) artış olduğu görülür.
c) 14 m³ su kullanan ev ile 16 m³ su kullanan ev arasındaki fatura farkını hesaplayınız.
f(14) = 28·14 + 20 = 412 TL
f(16) = 48·16 − 280 = 488 TL
Fatura farkı = 488 − 412 = 76 TL
Sonuç: 16 m³ su kullanan ev, 14 m³ su kullanan evden 76 TL daha fazla fatura öder.
16. Soru – Yeryüzünden yükseklere çıkıldıkça her 200 metrede hava sıcaklığı 1°C azalmaktadır. Bir dağcı ekibi, tırmanma öncesi sıcaklık ölçümü yapmak için doğrusal bir rotada gökyüzü ile yeryüzü arasında sabit hızla hareket eden bir uçangöz uçurmaktadır. Uçangözün yaptığı ölçümlerde o andaki konumunun yerden yüksekliği ile o yükseklikteki sıcaklık değeri hesaplanmaktadır
a) Görselde boş bırakılan deniz seviyesindeki sıcaklık değeri ve dağın yüksekliğini belirleyiniz.
Verilen bilgilere göre:
2400 m’de sıcaklık 1 °C,
3200 m’de sıcaklık −3 °C.
Yani 800 m yükselmede sıcaklık 4 °C azalmış → her 200 m’de 1 °C kuralına uygundur.
Bu durumda:
2400 m’de 1 °C → deniz seviyesinde (0 m) sıcaklık 13 °C olur (çünkü 2400 m / 200 m = 12 kademede 12 °C fark).
Dağın en yüksek noktası: 3200 m.
Sonuç: Deniz seviyesindeki sıcaklık 13 °C, dağın yüksekliği 3200 m.
b) Ölçümler sırasında uçangözün dakikadaki hızı kaç metredir?
Uçangöz II’den III’e 5 dakikada 2400 m → 3200 m çıkar, yani 800 m yükselir.
Dakikadaki hız: 800 ÷ 5 = 160 m/dk.
Cevap: 160 m/dk.
c) I’den III’e çıkıp hiç durmadan tekrar I’e dönüyor. Zirveye uzaklığın (m) zamana bağlı (dk.) değişimini ifade eden fonksiyon ve grafik
Gidiş-dönüş toplam 40 dk; her dakika 160 m’lik değişim var.
Fonksiyon (düz font): f(x) = 3200 − |160x − 3200|, 0 ≤ x ≤ 40.
Grafik: x=0 ve x=40’ta 0, x=20’de 3200 (V-şekli).
17. Soru – Deposunda 55 litre yakıt olan bir aracın zamana (sa.) bağlı aldığı yol (km) aşağıdaki doğrusal grafikte verilmiştir.
Verilenler:
- Depoda 55 L yakıt var.
- 0–5 saatte hız 80 km/sa (grafikte 0→5 saatte 400 km).
- 5–10 saatte hız 100 km/sa (5→10 saatte 500 km).
- 10. saatten sonra hız 90 km/sa.
- Sarfiyat tablosu (l/sa): 90 km/sa = 5, her +5 km/sa için +0,5, her −5 km/sa için −0,5.
Yakıt tüketimi:
-
80 km/sa: 4 L/sa ⇒ 5 saatte 20 L
-
100 km/sa: 6 L/sa ⇒ 5 saatte 30 L
İlk 10 saatte 50 L biter, 5 L kalır. -
Sonra 90 km/sa ve 5 L/sa ⇒ 1 saat daha gider.
Mesafe:
- 0–5 s: 5×80 = 400 km
- 5–10 s: 5×100 = 500 km
- 10–11 s: 1×90 = 90 km
Toplam: 400 + 500 + 90 = 990 km.
Cevap: 990 km (C).
18. Soru – Fabrikada A Ham Maddesi ve B Ürünü
Soru: A ham maddesinin stoğu doğrusal olarak 600’den 0’a (100. günde) düşüyor. B ürününün stoğu da doğrusal artıyor. A bittiğinde B üretimi duruyor. A ve B’nin zamana bağlı değişimleri grafikte verilmiş.
a) “A ham maddesi tükendiği anda üretilen B maddesinin stok sayısı kaçtır?”
A, 100. günde biter. Grafikten t=100 noktasında B = 300 okunur.
Cevap: 300.
b) “Bir sonraki üretimde 500 adet B maddesi üretilmek istenirse A stoku kaç olmalıdır?”
Grafikten eğimler:
- A: 600 → 0 (100 günde) ⇒ günlük 6 birim harcanır.
- B: 0 → 300 (100 günde) ⇒ günlük 3 birim üretilir.
500 adet B için gereken süre: t = 500 / 3 = 166,7 gün.
Bu sürede gereken A: 6 · 166,7 ≈ 1000.
Cevap: 1000.
19. Soru – Mutlak Değerli Eşitsizlik
n pozitif tam sayı. fₙ(x) = x − n.
|f₂(x)| ≤ |f₈(x)| koşulunu sağlayan pozitif tam sayı x’lerin toplamı?
Çözüm
|x−2| ≤ |x−8| iki noktaya uzaklık karşılaştırmasıdır. 2 ile 8’in orta noktası 5 olduğundan, x ≤ 5 olan tüm değerler eşitsizliği sağlar.
Pozitif tam sayılar: 1, 2, 3, 4, 5 → toplam 15.
Cevap: 15.
20. Soru – Aşağıdaki önermelerden hangisinin doğru olduğunu öğrencilerine soruyor.
Önerme I: b < 0 ve f artan (a > 0) ise kök x0 = −b/a > 0 olur → doğru.
Önerme II: “b < −b/a ise f artandır.” Koşul, a’nın işaretini garanti etmez (a < 0 iken de sağlanabilir) → yanlış.
Önerme III: a > 0 ve b < 0 iken, tüm x ∈ (−∞, −b/a) için f(x) < 0 olur → doğru.
Sonuç: I ve III doğru ⇒ D.
21. Soru – Hasan ve Sevgi’nin aynı grafikleri elde ettikleri bilindiğine göre a + b ifadesinin değeri kaçtır?
Verilenler:
- Hasan: f(x) = { −b x + 10 , x ≤ 3a − 1 ; b x − 10 , x > 5a − 5 }
- Sevgi: g(x) = |10 − b x| = { −b x + 10 , x ≤ 10/b ; b x − 10 , x ≥ 10/b }
Aynı grafik için kırılma noktaları eşit olmalı:
3a − 1 = 5a − 5 = 10/b.
Buradan: 3a − 1 = 5a − 5 ⇒ a = 2.
10/b = 3a − 1 = 5 ⇒ b = 2.
a + b = 2 + 2 = 4 ⇒ A.






Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.