9. Sınıf Matematik 1. Ders Kitabı Sayfa 159-160 Cevapları Meb Yayınları

9. Sınıf Matematik 1. Ders Kitabı Sayfa 159 Cevapları (MEB Yayınları)
1-4. soruları aşağıdaki bilgilerden yararlanarak cevaplayınız.
Bir firma, veri güvenliğini sağlamak amacıyla virüs koruma programı satın almak istemektedir. Firmanın incelediği M ve N programlarının kurulum ve aylık kullanım ücretleri (TL) aşağıdaki tabloda verilmiştir:
| Program | Kurulum Ücreti (TL) | Aylık Ücret (TL) |
|---|---|---|
| M | 1500 | 200 |
| N | 600 | 250 |
Soru 1: M programı için kullanım süresine bağlı (ay) ödenecek ücreti gösteren fonksiyon f, N programı için kullanım süresine bağlı (ay) ödenecek ücreti gösteren fonksiyon g tanımlayın ve cebirsel temsillerini yazın.
M programı (f):
Tanım kümesi: [0, ∞), Görüntü kümesi: [1500, ∞)
Cebirsel temsil: f(x) = 1500 + 200x
N programı (g):
Tanım kümesi: [0, ∞), Görüntü kümesi: [600, ∞)
Cebirsel temsil: g(x) = 600 + 250x
Soru 2: Firma, satın aldığı virüs koruma programını 1 yıl kullanacaktır. Firmanın hangi programı seçmesinin daha ekonomik olacağını belirleyiniz.
Cevap: Kullanım süresi: x = 12 ay
f(12) = 1500 + 200 × 12 = 1500 + 2400 = 3900 TL
g(12) = 600 + 250 × 12 = 600 + 3000 = 3600 TL
Sonuç: 12 aylık kullanımda N programı daha ekonomiktir.
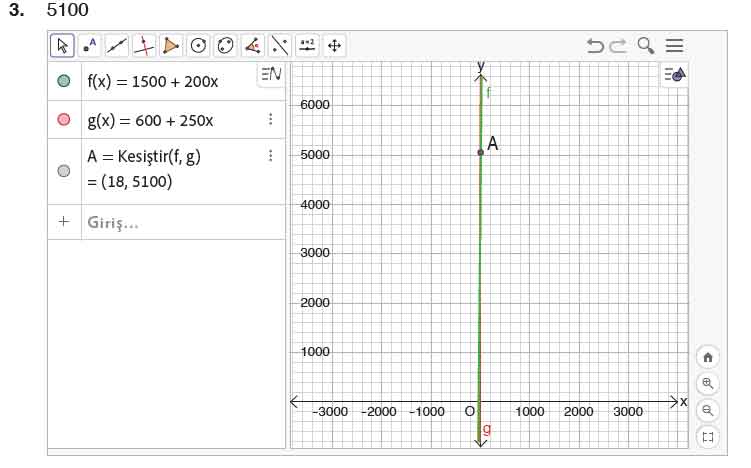
Soru 3: Matematik yazılımı yardımıyla f ve g fonksiyonlarının grafiklerini çizerek iki program için ödenecek ücretin kaç ay sonunda eşitlendiğini bulunuz.
Cevap: Fonksiyonlar eşit olmalıdır:
Eşitlik için: f(x) = g(x)
1500 + 200x = 600 + 250x
900 = 50x
x = 18 ay
Eşitlenme durumu: f(18) = 1500 + 200 × 18
f(18) = 1500 + 3600 = 5100 TL
Sonuç: İki program için ödenecek ücret 18. ayda 5100 TL değerinde eşitlenir.
Soru 4: İki programa ödenecek ücretin kaç aylık kullanım sonunda birbirine eşit olacağını bulunuz.
Cevap: Eşitlik için: f(x) = g(x)
1500 + 200x = 600 + 250x
900 = 50x
x = 18 ay
Sonuç: İki programa ödenecek ücret 18. ayda birbirine eşit olur.
5-6. Sorular ve Cevaplar
Soru 5: Asansörün aşırı yüklenmesini önlemek amacıyla bir uyarı yazısı hazırlanacaktır. Asansörde binen kişilerin toplam kütlesini (kg) gösteren bir eşitsizlik yazınız.
Cevap: Asansörün kapasitesi 720 kg'dir. Çocukların toplam kütlesi: 30 * y ve yetişkinlerin toplam kütlesi: 80 * x.
Asansöre x tane çocuk (30 kg) ve 1 yetişkin (80 kg) binmektedir.
Eşitsizlik: 30x + 80 ≤ 720
Sonuç: Aşırı yükleme durumunu önlemek için, yukarıdaki eşitsizlik sağlanmalıdır.
Soru 6: Asansörün refakatçi ile birlikte en fazla kaç çocuğu taşıyabileceğini bulunuz.
Cevap: Refakatçi yetişkin olduğundan 1 yetişkin = 80 kg:
Asansöre x tane çocuk (30 kg) ve 1 yetişkin (80 kg) binmektedir. Eşitsizlik şu şekilde yazılır:
30x + 80 ≤ 720
80’i diğer tarafa geçirerek:
30x ≤ 720 - 80
30x ≤ 640
Her iki tarafı 30’a bölerek:
x ≤ 640 ÷ 30
x ≤ 21,33
Sonuç: En fazla 21 çocuk asansöre binebilir.
Soru 7: Doruk’un zamana (t) bağlı okula olan mesafesini (d) modelleyen fonksiyonu cebirsel ve grafik temsiliyle ifade ediniz.
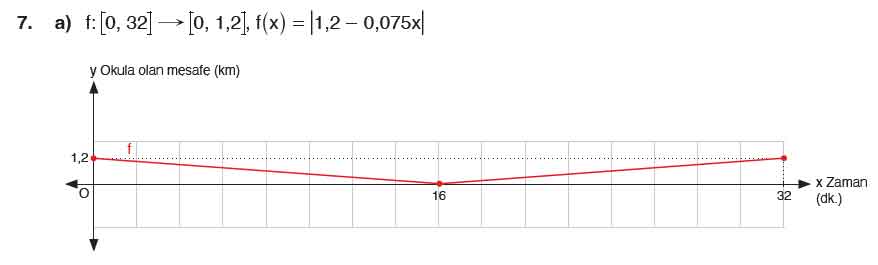
Soru (a): Doruk'un zamana (dk.) bağlı okula olan mesafesini (km) modelleyen fonksiyonu cebirsel ve grafik temsiliyle ifade ediniz.
Cevap (a): Doruk sabit hızla yürüdüğü için doğrusal bir hareket modeli kullanılır:
- Gidiş için fonksiyon: f(t) = 1,2 - (1,2 / 16) * t (0 ≤ t ≤ 16)
- Dönüş için fonksiyon: g(t) = (1,2 / 16) * (t - 16) (16 ≤ t ≤ 32)
Grafikte gidiş azalan, dönüş artan bir doğrusal hareket olarak ifade edilir.
Soru (b): Doruk’un okula olan mesafesinin 400 metreden az olduğu saat aralığını belirleyecek çözüm stratejileri oluşturunuz.
Cevap (b): Doruk’un mesafesinin 400 metre (0,4 km) olduğu durumu çözmek için:
- Gidiş için: f(t) < 0,4 çözülür.
- Dönüş için: g(t) < 0,4 çözülür.
Soru (c): Belirlediğiniz stratejileri kullanarak problemi çözünüz.
Doruk'un mesafesinin 400 metreden (0,4 km) az olduğu durumu inceleyelim:
Mesafeyi tanımlayan eşitsizlik:
-1,2 < 1,2 - 0,075x < 0,4
Eşitsizliği çözmek:
İlk eşitsizlik:
1,2 - 0,075x > 0,4
-0,075x > -0,8
x < 10,6
İkinci eşitsizlik:
1,2 - 0,075x < 0,4
-0,075x < -0,8
x > 21,3
Sonuç: Çözüm aralığı: 10,6 < x < 21,3
Bu aralık, Doruk'un mesafesinin 400 metreden az olduğu zaman dilimini ifade eder.
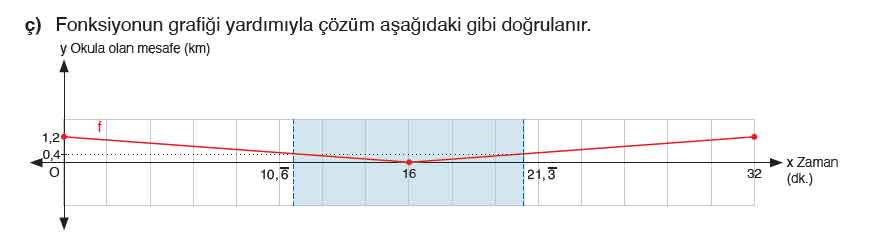
ç) Elde ettiğiniz çözümü farklı yöntemlerle doğrulayınız.
- Verilen eşitsizlik çözümü ile zaman aralığını elde ettik: 10,6 dakika (08:11) ile 21,3 dakika (08:21) arasında.
- Bu zaman aralığında Doruk'un okula olan mesafesi 400 metreden azdır.
Soru d): Problemin farklı çözüm yöntemlerini ilişkilendirerek elde ettiğiniz çıkarımları değerlendiriniz.
Cevap d): Doruk’un okula olan mesafesi 0,4 km’den küçüktür x ∈ (10,6̅ , 21,3̅) dakikaları arasında.
Saat 08.00 başlangıç alınırsa:
- Alt sınır: 08:00 + 10,7 dk ≈ 08:11,
- Üst sınır: 08:00 + 21,3 dk ≈ 08:21.
Sonuç: Doruk, 08:11–08:21 arasında okula 400 m’den daha yakın bir konumdadır.





Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.