9. Sınıf Matematik 1. Ders Kitabı Sayfa 135 Cevapları Meb Yayınları

9. Sınıf Matematik 1. Ders Kitabı Sayfa 135 Cevapları (MEB Yayınları)

Konu: Mutlak Değer Fonksiyonları – Alıştırmalar

1. Elektrik devrelerinde kullanılan dirençler konulu soru

Soru: Elektrik devre elemanları satışı yapan bir firma, 680 ohm ± %5 değerinde dirençler üretmektedir.
Üretilen dirençlerin gerçek değerine (ohm) bağlı hata miktarını (ohm) ifade eden f fonksiyonunun cebirsel temsilini bulunuz ve fonksiyonun grafiğini çiziniz.

Cevap – a)

%5 tolerans = 680 × 0,05 = 34 ohm
Gerçek değer x (ohm) olduğunda hata miktarı:
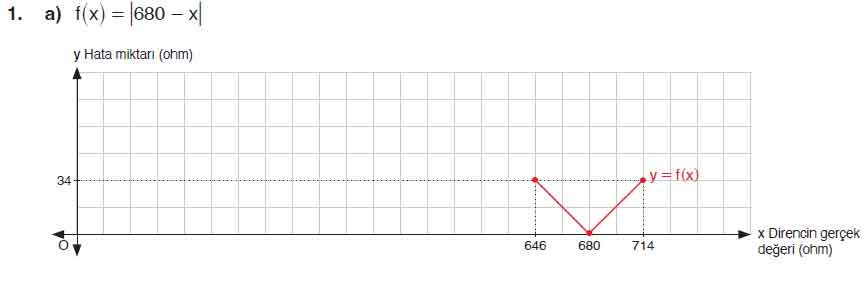
f(x) = |680 − x|

Tanım Kümesi: [680 − 34, 680 + 34] → [646, 714]
Görüntü Kümesi: [0, 34]

Grafik: V şeklinde bir grafik olup tepe noktası (680, 0)’dır.
x=646 ve x=714 noktalarında f(x)=34 olur.
Fonksiyon [646,680] aralığında azalan, [680,714] aralığında artan bir grafiğe sahiptir.

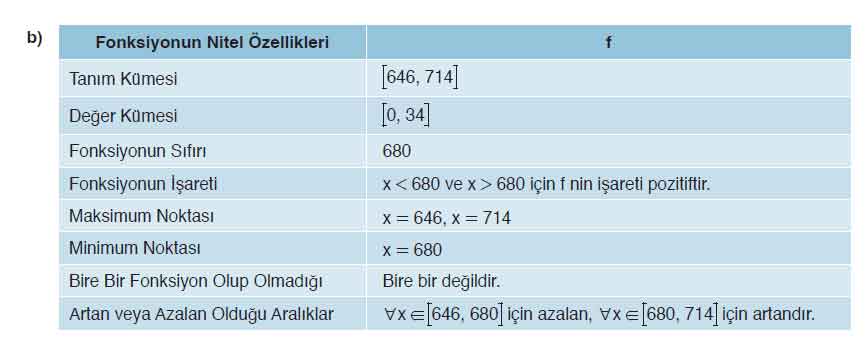
Cevap – b)

Aşağıdaki tabloyu elde ettiğiniz f fonksiyonunun nitel özelliklerine göre doldurunuz:

2. f(x)=1−2x ve g(x)=|f(x)|−3 fonksiyonlarıyla ilgili soru

Soru: Gerçek sayılarda f(x)=1−2x ve g(x)=|f(x)|−3 şeklinde tanımlı fonksiyonlar veriliyor.
g fonksiyonuna göre aşağıdaki soruları cevaplayınız.

a) Görüntü kümesini bulunuz.

|1−2x| ≥ 0 olduğu için, |1−2x|−3 ≥ −3 olur.
Dolayısıyla g(x) ∈ [−3, ∞)

Cevap: Görüntü kümesi = [−3, ∞)

b) Sıfırlarını bulunuz.

g(x)=|1−2x|−3=0
⇒ |1−2x|=3
1−2x=3 → x=−1
1−2x=−3 → x=2

Cevap: x₁=−1, x₂=2

c) Artan veya azalan olduğu aralıkları bulunuz.

Kırılma noktası: |1−2x|’in içi sıfır olduğunda, 1−2x=0 → x=1/2

• x ≤ 1/2 için g(x)=−2x−2 → azalan
• x ≥ 1/2 için g(x)=2x−4 → artan

Cevap: (−∞, 1/2] aralığında azalan,
[1/2, ∞) aralığında artan

ç) Minimum ve maksimum değerlerini bulunuz.

|1−2x| en az 0 olduğunda (x=1/2):
g(1/2)=0−3=−3 → minimum değer −3’tür.

Fonksiyon pozitif yönde sınırsız büyüdüğünden maksimum değer yoktur.

Cevap: Minimum = −3 (x=1/2)
Maksimum = yoktur