9. Sınıf Matematik 1. Ders Kitabı Sayfa 124-126 Cevapları Meb Yayınları

9. Sınıf Matematik Ders Kitabı Sayfa 124 Cevapları (MEB Yayınları)
7. Uygulama – Mutlak Değer Fonksiyonları
a) Ölçülen vücut sıcaklığına bağlı ortalamadan sapma miktarının bağımlı ve bağımsız değişkenlerini sözel olarak ifade ediniz.
Cevap: Bu durumda bağımsız değişken, ölçülen vücut sıcaklığıdır (°C).
Bağımlı değişken ise, bu sıcaklığın ortalama değer olan 36,5 °C’den ne kadar sapma gösterdiğini ifade eden sapma miktarıdır (°C).
Yani, sapma miktarı ölçülen vücut sıcaklığına bağımlıdır.
b) Bağımlı ve bağımsız değişkenler hangi değerleri alabilir? Aralık şeklinde ifade ediniz.
- Bağımsız değişken (x): 35,7 °C ≤ x ≤ 37,5 °C
- Bağımlı değişken (|x − 36,5|): 0 °C ≤ |x − 36,5| ≤ 1 °C
Bu aralıklar, sağlıklı bir insanın normal vücut sıcaklığı ve ondan olan sapma miktarını göstermektedir.
c) Sağlıklı bir bireyin vücut sıcaklığına bağlı (x) ortalamadan sapma miktarını ifade eden g fonksiyonunun cebirsel temsilini yazınız.
Cevap: g(x) = |x − 36,5|
Bu fonksiyon, ölçülen vücut sıcaklığının ortalama sıcaklık olan 36,5 °C’den mutlak farkını (sapmasını) gösterir.
Yani sıcaklık ortalamanın üstünde ya da altında olsa da sonuç daima pozitif çıkar.
| Değişken Türü | Anlamı | Aralık |
|---|---|---|
| Bağımsız Değişken (x) | Ölçülen vücut sıcaklığı | 35,7 °C ≤ x ≤ 37,5 °C |
| Bağımlı Değişken (g(x)) | Ortalamadan sapma miktarı | 0 °C ≤ g(x) ≤ 1 °C |
9. Sınıf Matematik Ders Kitabı Sayfa 125 Cevapları (MEB Yayınları)
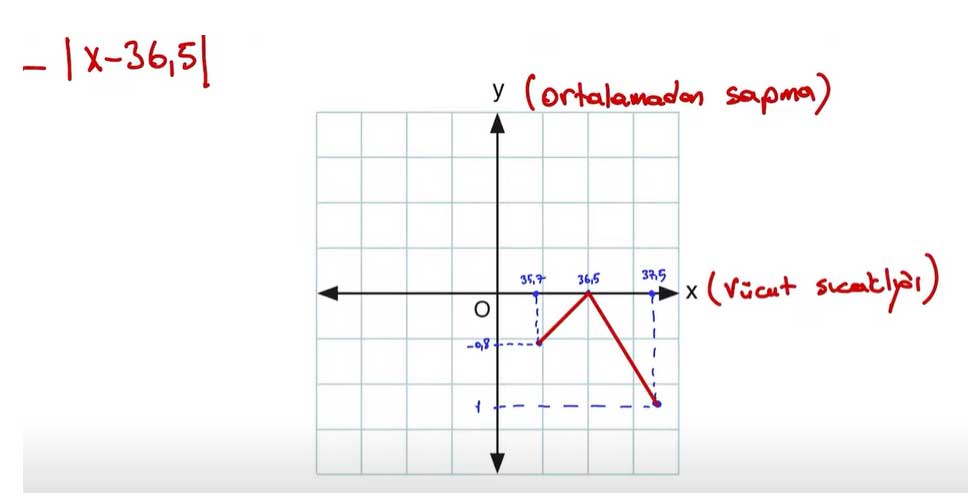
ç) Elde ettiğiniz sonuçlardan yararlanarak g fonksiyonunun grafiğini çiziniz.
Cevap: Fonksiyonumuz: g(x) = |x − 36,5|
Bu fonksiyonun grafiği, tepe noktası (36,5, 0) olan V şeklinde bir mutlak değer grafiğidir.
Grafik, x eksenine göre simetriktir ve x = 36,5 noktasında minimum değeri 0’dır.
Grafik Açıklaması:
- x = 35,5 → g(x) = 1
- x = 36 → g(x) = 0,5
- x = 36,5 → g(x) = 0
- x = 37 → g(x) = 0,5
- x = 37,5 → g(x) = 1
Bu değerler grafiğe yerleştirildiğinde “V” şeklinde bir mutlak değer eğrisi oluşur.
2. g fonksiyonunun cebirsel temsilinin −1 ile çarpılmasıyla elde edilen fonksiyon h olsun. Gerçek sayılarda tanımlı h fonksiyonunun cebirsel temsilini yazarak grafiğini çiziniz.
g(x) = |x − 36,5| olduğuna göre,
h(x) = −g(x) = −|x − 36,5| olur.
Bu durumda h fonksiyonunun grafiği, g(x) grafiğinin x-ekseni altına simetrik yansımasıdır.
Yani yine tepe noktası (36,5, 0) olur; fakat grafik aşağıya dönük bir V şekli alır.
8. Uygulama – Mutlak Değer Fonksiyonlarının Nitel Özellikleri
Verilen üç grafik:
- Grafik 1: f(x) = ax + b
- Grafik 2: g(x) = |ax + b|
- Grafik 3: h(x) = −|ax + b|
1. a) f ve g fonksiyonlarının cebirsel ve grafiksel benzerliklerini, farklılıklarını gözlemleyiniz.
Benzerlik:
Her iki fonksiyonda da “ax + b” ifadesi vardır. Yani doğrusal ifadenin mutlak değeri alınmıştır.
Farklılık:
f(x) grafiği doğrusal bir fonksiyondur, g(x) ise mutlak değerli olduğu için V şeklindedir.
f(x)’in negatif kısmı x-ekseni altındayken, g(x)’te bu kısım x-ekseni üstüne yansır.
b) f ve h fonksiyonlarının cebirsel ve grafiksel benzerliklerini, farklılıklarını gözlemleyiniz.
Benzerlik: Her ikisinde de “ax + b” ifadesi bulunur.
Farklılık:
f(x) = ax + b doğrusal bir fonksiyon iken,
h(x) = −|ax + b| grafiği aşağıya dönük V şeklinde bir mutlak değer grafiğidir.
Yani g(x)’in x-ekseni altına yansıtılmış hâlidir.
9. Sınıf Matematik Ders Kitabı Sayfa 126 Cevapları (MEB Yayınları)
2. f, g ve h fonksiyonlarının nitel özelliklerini tabloya yazınız.
| Fonksiyonun Nitel Özellikleri | f(x) = ax + b | g(x) = |ax + b| | h(x) = −|ax + b| |
|---|---|---|---|
| En Geniş Tanım Kümesi | ℝ | ℝ | ℝ |
| Görüntü Kümesi | ℝ | [0, +∞) | (-∞, 0] |
| Fonksiyonun Sıfırı | ax + b = 0 → x = -b/a | ax + b = 0 → x = -b/a | ax + b = 0 → x = -b/a |
| Fonksiyonun İşareti | ax + b’ye göre + / − | ≥ 0 (daima) | ≤ 0 (daima) |
| Maksimum Noktası | Yok | Yok | Tepe noktası (maks.) |
| Minimum Noktası | Yok | Tepe noktası (min.) | Yok |
| Bire Birlik | Bire bir | Bire bir değil | Bire bir değil |
| Artan / Azalan Aralıklar | a > 0 → artan, a < 0 → azalan | x < -b/a → azalan, x > -b/a → artan | x < -b/a → artan, x > -b/a → azalan |
3. Elde ettiğiniz nitel özelliklerden yararlanarak g ve h mutlak değer fonksiyonlarının parçalı gösterimine dair çıkarımlarınızı açıklayınız.
Cevap: Mutlak değerli fonksiyonlar, mutlak değerin tanımından dolayı parçalı olarak ifade edilir:
g(x) = |ax + b| için:
g(x) = { ax + b , eğer ax + b ≥ 0
−(ax + b) , eğer ax + b < 0
h(x) = −|ax + b| için:
h(x) = { −(ax + b) , eğer ax + b ≥ 0
ax + b , eğer ax + b < 0
Bu gösterim, fonksiyonun x = −b/a noktasında yön değiştirdiğini ve grafiğin bu noktada simetri oluşturduğunu gösterir.





Türkçe karakter kullanılmayan ve büyük harflerle yazılmış yorumlar onaylanmamaktadır.