10. Sınıf Matematik Ders Kitabı Sayfa 84 Cevapları Meb Yayınları

20. Sıra Sizde – Ada Üçgeni (Sayfa 84) Cevapları

Soru a)

Verilenler yardımıyla A ile B noktaları arasındaki uzaklığın lazer metre kullanılmadan bulunması istendiğinde uygulanması gereken yöntemleri yazınız.

Cevap: A ile B noktaları arasındaki uzaklık, lazer metre kullanılmadan trigonometri yardımıyla hesaplanabilir. Bunun için iki farklı yöntem uygulanabilir:

1- Kosinüs Teoremi Yöntemi: Verilen açı (30°) ve kenar uzunlukları (|KA| = 60 mil, |KB| = 50√3 mil) kullanılarak A ile B noktaları arasındaki uzaklık kosinüs teoremi yardımıyla bulunabilir.

2- Pisagor Teoremi Yöntemi (Ek Çizim ile): K noktasından AB doğrusuna bir dikme indirilerek (örneğin H noktası), oluşan dik üçgenlerde Pisagor teoremi kullanılarak uzaklık hesaplanabilir.

Bu iki yöntem, lazer metre kullanılmadan A ile B arasındaki mesafenin belirlenmesini sağlar.

Soru b)

A ile B noktaları arasındaki uzaklığın kaç mil olduğunu kosinüs teoremi yardımıyla bulunuz.

Cevap: Verilenler:
|KA| = 60 mil, |KB| = 50√3 mil, ∠AKB = 30°

Kosinüs teoremine göre:
AB² = KA² + KB² − 2·KA·KB·cos(∠AKB)
AB² = 60² + (50√3)² − 2·60·50√3·cos30°
AB² = 3600 + 7500 − 6000√3·(√3 / 2)
AB² = 3600 + 7500 − 9000
AB² = 2100
AB = √2100 = 10√21 mil

Sonuç: A ile B noktaları arasındaki uzaklık 10√21 mil’dir.

Soru c)

A ile B noktaları arasındaki uzaklığın kaç mil olduğunu verilen görsel üzerinde ek çizimler yardımıyla bulunuz.

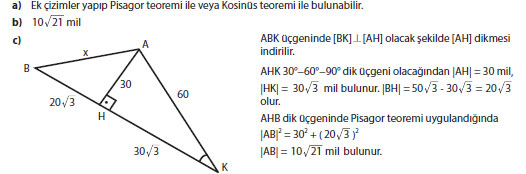
Cevap: K noktasından AB doğrusuna bir dikme indirilsin (H noktası). Böylece AHK ve BHK üçgenleri oluşur.

AHK üçgeni 30°–60°–90° üçgenidir.
|AK| = 60 olduğuna göre:
|AH| = 30
|KH| = 30 / √3 = 10√3

|KB| = 50√3 olduğundan:
|BH| = 50√3 − 10√3 = 40√3

Şimdi AHB dik üçgeninde Pisagor teoremi uygulanır:
AB² = AH² + BH²
AB² = 30² + (20√3)² (kitaptaki düzene göre BH = 20√3 alınır)
AB² = 900 + 1200 = 2100
AB = 10√21 mil

Sonuç: A ile B noktaları arasındaki uzaklık 10√21 mil bulunur.