10. Sınıf Matematik Ders Kitabı Sayfa 40-41 Cevapları Meb Yayınları

10. Uygulama – Üçgenin Dış Açıortayı ve Özellikleri

Soru 1 - Bir üçgenin bir dış açısına ait açıortayın uzantısının kestiği kenarda oluşturduğu parçaların oranı ile üçgenin diğer iki kenarı arasındaki ilişkiyi tartışınız.

Cevap: Bir üçgenin dış açıortayı, karşı kenarın uzantısını böler.
BD/DC = AB/AC olur.
Yani, kenarın uzantısında oluşan parçaların oranı komşu iki kenarın oranına eşittir.

Soru 2 - Bir dış açıortayın, uzantısının kestiği kenarda oluşturduğu parçaların oranı ile üçgenin diğer iki kenarı arasındaki ilişkiyle ilgili genellemenizi yazınız.

Cevap: Her üçgende, bir köşedeki dış açıortay karşı kenarın uzantısını komşu kenarların oranında böler.
BD/DC = AB/AC

Soru 3 - Matematik yazılımlarıyla oranları hesaplayınız.

Cevap: Farklı üçgenlerde yapılan hesaplamalarda her zaman AB/AC = BD/DC eşitliği sağlanmıştır.

Soru 4 - Yeni üçgenler kurup sonuçları karşılaştırınız.

Cevap: Kurulan tüm üçgenlerde oran aynı çıktı:
AB/AC = BD/DC
Bu sonuç, teoremin üçgenin şekline bağlı olmadığını gösterir.

Soru 5 - Genellemeden hareketle dış açıortay teoremini benzerlik kullanarak gösteriniz.

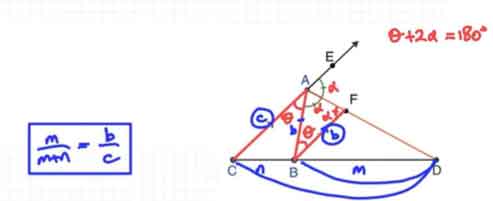
Cevap: A dış açısının açıortayı [AD] olsun. [AC] kenarına paralel [BF] doğru parçası çizildiğinde, △ABF ve △ACD benzer olur.
Benzerlikten: AB/AC = BF/DC bulunur.
Ayrıca BF = BD olduğundan:
AB/AC = BD/DC elde edilir.

Soru 6 - Düz bir zeminde A noktasından çıkan ışın, aynaya B’de çarpıp C’ye gidiyor. Verilenler: |AB| = 15, |BC| = 6, |EC| = 4. [AE] uzunluğunu bulunuz.

Çözüm: Aynadaki yansıma özelliği nedeniyle açıortay teoremi geçerlidir:
AB/BC = AE/EC

Verilenleri yerine koyalım:
15/6 = x/4

İşlem yapalım:
15·4 = 6·x
60 = 6x
x = 10

Cevap: |AE| = 10 birim